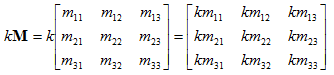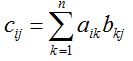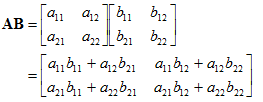标量和矩阵的乘法

直接用这个标量乘以矩阵的每一项

矩阵与矩阵相乘

如果矩阵A的列数和B的行数不匹配，则乘法AB无意义。

矩阵乘法计算如下：记r×n矩阵A与n×c矩阵B的积r×c矩阵AB为C。C的任意元素Cij等于A的第i行向量与B的第j列向量的点乘结果。正式定义为：

例如

关于矩阵乘法的注意事项：
任意矩阵M乘以方阵S，不管从哪边乘，都将得到与原矩阵大小相同的矩阵。当然，前提是假定乘法有意义。如果S是单位矩阵，结果将是原矩阵M，即MI=IM=M

• 矩阵乘法不满足交换律，即：AB≠BA
• 矩阵乘法满足结合律，即：(AB)C=A(BC)。(假设A，B，C的维数使其乘法有意义，要注意如果(AB)C有意义，那么A(BC)一定也有意义。)矩阵乘法结合律可以扩展到多个矩阵的情况下，如：ABCDEF=((((AB)C)D)E)F=A((((BC)D)E)F)=(AB)(CD)(EF)

注意所有括法都能计算出正确结果，但有些组中标量乘法更少。寻找使标量乘法最少的括法的问题称作：矩阵链问题。

• 矩阵乘法也满足与标量或向量的结合律，即：(kA)B=k(AB)=A(kB)、(vA)B=v(AB)
• 矩阵积的转置相当于先转置矩阵然后以相反的顺序乘：(AB)^T=B^TA^T

这一结论可以扩展到多个矩阵的情形：

哈达玛(Hadamard)乘积

对于相同形状的矩阵A、B，将相同位置的元素相乘，由此产生的矩阵称为矩阵A、B的Hadamard乘积，用A⊙B表示。