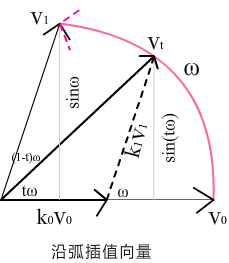
沿弧插值向量
post by:追风剑情 2016-11-5 15:35
设两个2D向量V0和V1,都是单位向量。我们要计算Vt,它是沿V0到V1弧的平滑插值。设ω是V0到V1弧所截的角,那么Vt就是绕V1沿弧放置tω的结果。如图
将Vt表达成V0和V1的线性组合,从另一方面说,存在两个非零常数k0和k1,使得:
vt=k0v0+k1v1
可以用基本几何学求出k0和k1。
对以k1v1为斜边的直角三角形应用三角公式得:
sinω=sin(tω)/k1 => k1=sin(tω)/sinω
用同样的方法求得k0:
k0=sin(1-t)ω/sinω
vt可以表示为:
vt=k0v0+k1v1
vt=(sin(1-t)ω/sinω)v0 + (sintω/sinω)v1 (沿弧插值向量公式)
评论:
发表评论: