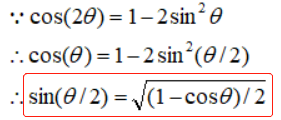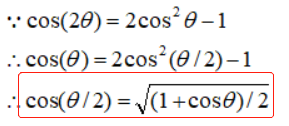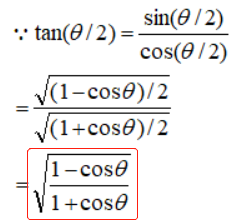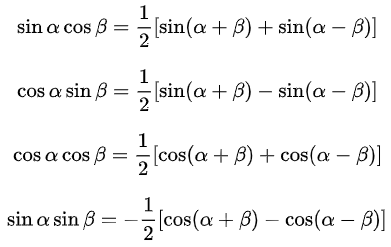公式总结
secθ=1/cosθ
cscθ=1/sinθ
cotθ=1/tanθ
sin²θ+cos²θ=1
1+tan²θ=sec²θ
1+cot²θ=csc²θ
sin(-θ)=-sinθ
cos(-θ)=cosθ
tan(-θ)=-tanθ
sin(π/2-θ)=cosθ
cos(π/2-θ)=sinθ
tan(π/2-θ)=cotθ

和角差角公式：

sin(x+y)=sinxcosy+cosxsiny
sin(x-y)=sinxcosy-cosxsiny
cos(x+y)=cosxcosy-sinxsiny
cos(x-y)=cosxcosy+sinxsiny
tan(x+y)=(tanx+tany)/(1-tanxtany)
tan(x-y)=(tanx-tany)/(1+tanxtany)

倍角公式
sin(2θ)=2sinθcosθ
cos(2θ)=cos²θ-sin²θ=1-2sin²θ=2cos²θ-1
tan(2θ)=(2tanθ)/(1-tan²θ)

半角公式

积化和差公式

推导方式：将和差角公式左右两边加相或相减。
sin(x+y)+sin(x-y)=2sinxcosy
cos(x+y)+cos(x-y)=2cosxcosy

和差化积公式

三角形的内角与边

sinA/a=sinB/b=sinC/c
a²=b²+c²-2bccosA
b²=a²+c²-2accosB
c²=a²+b²-2abcosC

和差角公式的推导
转载 https://wenku.baidu.com/view/63fdb27ba31614791711cc7931b765ce04087a7d.html
单位圆

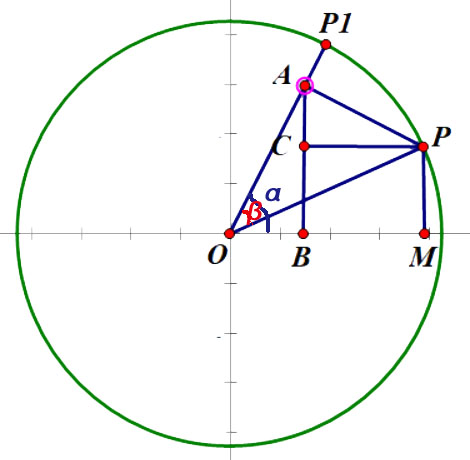
上图：已知 AB⊥OM，PM⊥OM，CP⊥AB，∠POP1=β，∠MOP1=α，|OP|=|OP1|=1，
OA=cosβ，AP=sinβ，OM=cos(α-β)
OM=OB+BM=OB+CP=OAcosα+APsinα=cosβcosa+sinβsina
综上所术 cos(α-β)=cosa.cosβ+sina.sinβ