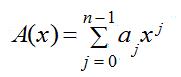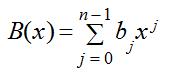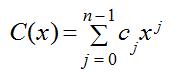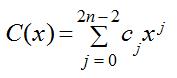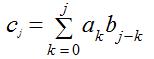多项式定义

一个以x为变量的多项式定义在一个代数域F上，将函数A(x)表示为形式和：

我们称a0,a1,...,an-1为如上多项式的系数，所有系数都属于域F，典型的情形是复数集合C。

如果一个多项式A(x)的最高次的非零系数是a_{k，则称A(x)的次数是k，记degree(A)=k。任何严格大于一个多项式次数的整数都是该多项式的次数界，因此对于次数界为n的多项式，其次数可以是0~n-1之间的任何整数，包括0和n-1。}

多项式相加

如果A(x)和B(x)是次数界为n的多项式，那么它们的和也是一个次数界为n的多项式C(x)，对所有属于定义域的x，都有C(x)=A(x)+B(x)。也就是说，若

和

则

其中对于j=0, 1, ..., n-1, 。例如，如果有多项式A(x)=6x³+7x²-10x+9和B(x)=-2x³+4x-5，那么C(x)=4x³+7x²-6x+4。

多项式相乘

如果A(x)和B(x)皆是次数界为n的多项式，则它们的乘积C(x)是一个次数界为2n-1的多项式，对所有属于定义域的x，都有C(x)=A(x)B(x)。

多项式相乘计算方式一：

把A(x)中的每一项与B(x)中的每一项相乘，然后再合并同类项。

多项式相乘计算方式二：

其中

例：A(x)=6x³+7x²-10x+9和B(x)=-2x³+4x-5;

C(x)=A(x)B(x)=-12x⁶-14x⁵+44x⁴-20x³-75x²+86x-45

注意，degree(C)=degree(A)+degree(B)，意味着如果A是次数界为n_a的多项式，B是次数界为n_b的多项式，那么C是次数界为n_a+n_b-1的多项式。因为一个次数界为k的多项式也是次数界为k+1的多项式，所以通常称乘积多项式C是一个次数界为n_a+n_b的多项多。