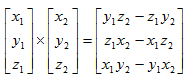计算矢量的叉积是判断直线和线段、线段和线段以及线段和点的位置关系的核心算法。假设有二维矢量P=(x1,y1), Q=(x2,y2)，则矢量的叉积定义为：

P×Q=x1*y2-x2*y1

      向量叉积的几何意义可以描述为由坐标原点(0,0)、P、Q和P+Q所组成的平行四边形的面积，而且是个带符号的面积，由此可知，矢量的叉积具有以下性质：

P×Q=－(Q×P)

      叉积的结果P×Q是P和Q所在平面的法矢量，它的方向是垂直于P和Q所在的平面，并且按照P、Q和P×Q的次序构成右手系，所以叉积的另一个非常重要性质是可以通过它的符号可以判断两矢量相互之间位置关系是顺时针还是逆时针关系，具体说明如下：

(1)如果P×Q>0，则Q在P的逆时针方向；

(2)如果P×Q<0，则Q在P的顺时针方向；

(3)如果P×Q=0，则Q与P共线(但可能方向是反的)。

给定向量P=(x1,y1)，Q=(x2,y2)，计算叉积的算法实现为：

double CrossProduct(double x1, double y1, double x2, double y2)
{
      return x1 * y2 - x2 * y1;
}

叉积不满足的运算律:
1、叉积不满足交换律，但它满足反交换律：a×b=-(b×a)
2、叉积不满足结合律，(a×b)×c≠a×(b×c)
3、(a●b)×c没有定义,因为标量和向量间不能叉乘

三重积

叉积3D坐标公式

叉积几何解释

||a×b||等于以a和b为两边的平行四边形的面积。