辗转相除的数学原理是朴素的欧几里得定理：

GCD(a, b) = GCD(b, a mod b)    (a mod b表示a除以b的余数)

代码实现

using System;
using System.Collections.Generic;
using System.Text;

namespace GCDTest
{
    class Program
    {
        static void Main(string[] args)
        {
            Console.WriteLine("{0}和{1}的最大公约数={2}", 28, 14, EuclidGcd(28, 14));
            Console.WriteLine("{0}和{1}的最大公约数={2}", 58, 14, EuclidGcd(58, 14));
            Console.WriteLine("{0}和{1}的最大公约数={2}", 99, 21, EuclidGcd(99, 21));

            Console.Read();
        }

        /// <summary>
        /// 辗转相除法求a和b的最大公约数
        /// </summary>
        public static int EuclidGcd(int a, int b)
        {
            if (b > a)
            {
                int tmp = a;
                a = b;
                b = tmp;
            }

            while (b != 0)
            {
                int tmp_b = b;
                b = a % b;
                a = tmp_b;
            }

            return a;
        }
    }
}

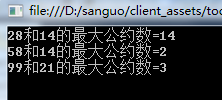
运行结果