蒙哥马利(Montgomery)幂模运算是快速计算a^b%k的一种算法，是RSA加密算法的核心之一。

数学原理

(a×b)%n = (a%n × b%n)%n

(a+b)%n = (a%n + b%n)%n

示例: 求a^9%n

a^9%n = (a^8 × a)%n = (a^8%n × a%n)%n

a^8%n = (a^4 × a^4)%n = (a^4%n × a^4%n)%n

a^4%n = (a^2 × a^2)%n = (a^2%n × a^2%n)%n

a^2%n = (a × a)%n = (a%n × a%n)%n

a%n = (1 × a)%n = (1%n × a%n)%n = (a%n)%n

C#代码实现

using System;

namespace MontgomeryTest
{
    class Program
    {
        static void Main(string[] args)
        {
            //测试数据
            int M = 7900000, E = 3, N = 9;
            //普通算法
            double R1 = Math.Pow(M, E) % N;
            //蒙哥马利算法
            int R2 = ModularPower(M, E, N);

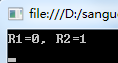
            Console.WriteLine("R1={0}, R2={1}", R1, R2);
            Console.Read();
        }

        /// <summary>
        /// 蒙哥马利幂模运算
        /// </summary>
        /// <param name="M">基数</param>
        /// <param name="E">指数</param>
        /// <param name="N">模数</param>
        /// <returns></returns>
        public static int ModularPower(int M, int E, int N)
        {
            int k = 1;
            int n = M % N;

            while (E > 0)
            {
                if ((E & 1) == 1)
                    k = (k * n) % N;

                n = (n * n) % N;

                E = E >> 1;
            }

            return k;
        }
    }
}

运行结果

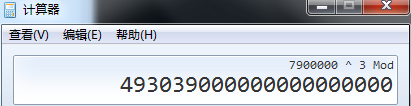
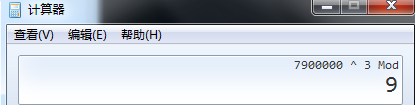
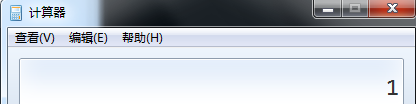
用科学计算器验证结果

结论: 当数据过大时无法用普通方法计算a^b%k