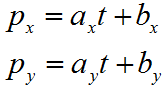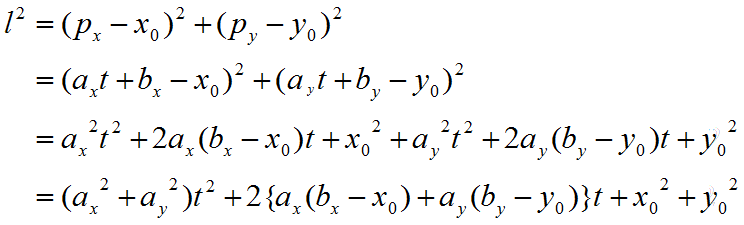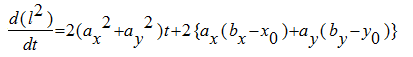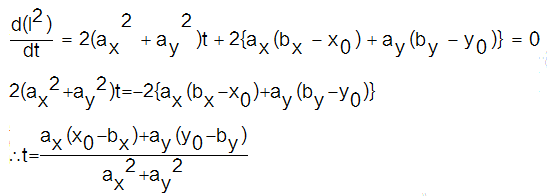线段的向量表示

p=at+b (0≤t≤1)

向量b为线段的起点，向量a是延着线段的向量。

问题：求点(x0, y0)到线段p的最短距离?

解题思路：将线段上的点p=at+b(0≤t≤1)与点(x0, y0)的距离表示为t的函数，然后对t进行微分，求得距离最小时的t。

向量p=at+b (0≤t≤1)可分解表示为:

设此线段上的点与点(x0, y0)的距离为l，根据勾股定理有:

上式中，令最小的t，就是点到线段的最短距离所对应的t。为了求的最小值，将等式用t进行微分，得到：

通过为零的t的值，我们就可以计算出线段与点的最短距离。下面让我们通过如下步骤求得t。