贪婪法(greedy algorithm)，又称贪心算法，是寻找最优解问题的常用方法。这种方法模式一般将求解过程分成若干个步骤，在每个步骤都应用贪心原则，选取当前状态下最好的或最优的选择(局部最有利的选择)，并以此希望最后堆叠出的结果也是最好或最优的解。贪婪法的每次决策都以当前情况为基础并根据某个最优原则进行选择，不从整体上考虑其他各种可能的情况。一般来说，这种贪心原则在各种算法模式中都会体现，单独作为一种方法来说明，是因为贪婪法对于特定的问题是非常有效的方法。

     贪婪法和动态规划法以及分治法一样，都需要对问题进行分解，定义最优解的子结构。但是，贪婪法与其他方法最大的不同在于，贪婪法每一步选择完之后，局部最优解就确定了，不再进行回溯处理，也就是说，每一个步骤的局部最优解确定以后，就不再修改，直到算法结束。因为不进行回溯处理，贪婪法只在很少的情况下可以得到真正的最优解，比如最短路径问题、图的最小生成树问题。大多数情况下，由于选择策略的“短视”，贪婪法会错过真正的最优解，得不到问题的真正答案。但是贪婪法简单高效，省去了为找最优解可能需要的穷举操作，可以得到与最优解比较接近的近似最优解，通常作为其他算法的辅助算法使用。

贪婪法的基本思想:

(1) 建立对问题精确描述的数学模型，包括定义最优解的模型；

(2) 将问题分解为一系列子问题，同时定义子问题的最优解结构；

(3) 应用贪心原则确定每个子问题的局部最优解，并根据最优解的模型，用子问题的局部最优解堆叠出全局最优解。

定义最优解的模型通常和定义子问题的最优解结构是同时进行的，最优解的模型一般都体现了最优解子问题的分解结构和堆叠方式。对于子问题的分解有多种方式，有的问题可以按照问题的求解过程一步一步地进行分解，每一步都在前一步的基础上选择当前最好的解，每做一次选择就将问题简化为一个规模更小的子问题，当最后一步的求解完成后就得到了全局最优解。还有的问题可以将问题分解成相对独立的几个子问题，对每个子问题求解完成后再按照一定的规则(比如某种公式或计算法则)将其组合起来得到全局最优解。

贪婪法
通过某个子问题的最优解达到全局最优解，往往得到的是近似最优解。

分治法
将大问题不断缩小成相同的小问题，当问题规模很小时很容易求解，可利用递归算法求解。

动态规划
自底向上求解，当前子问题的最优解作为下一个子问题的输入。

举例
能用数学归纳法表示的问题，可采用递归算法求解。(分治法)
能用数学递推公式表示的问题，可采用迭代算法求解。(动态规划)

示例: 求解0-1背包问题

      有N件物品和一个承重为C的背包，每件物品的重量是Wi，价值是Pi，求解将哪几件物品装入背包可使这些物品在重量总和不超过C的情况下价值总和最大。

贪婪策略1: 每次选择价值最高的物品放入背包。

贪婪策略2: 每次选择重量最轻的物品放入背包。

贪婪策略3: 每次选择价值密度最大的物品放入背包。(价值密度=价值/重量)

此示例采用贪婪策略1求解:

using System;
using System.Collections.Generic;

namespace BagProblemTest
{
    class Program
    {
        static void Main(string[] args)
        {
            //定义一组测试数据
            int[] w = new int[] { 35, 30, 60, 50, 40, 10, 25 };//重量
            int[] p = new int[] { 10, 40, 30, 50, 35, 40, 30 };//价值
            int C = 150;//背包最大能承受的重量

            BagProblem.Bag bag = new BagProblem.Bag();
            bag.totalC = C;
            for (int i = 0; i < w.Length; i++)
            {
                BagProblem.Item item = new BagProblem.Item();
                item.weight = w[i];
                item.price = p[i];
                bag.AddItem(item);
            }

            //求解
            new BagProblem().GreedyAlgo(bag);

            Console.Read();
        }
    }
}

/// <summary>
/// 背包问题类
/// </summary>
public class BagProblem
{
    //物品数据结构
    public class Item
    {
        public int weight;//重量
        public int price; //价值
        public int status;//状态(0:未选中 1:已选中 2:已经不可选)
    }

    //背包数据结构
    public class Bag
    {
        public List<Item> list = new List<Item>();//物品列表
        public int totalC;//能承受的总重量

        public void AddItem(Item item)
        {
            list.Add(item);
        }
    }

    /// <summary>
    /// 贪婪算法
    /// </summary>
    /// <param name="list">装有物品的背包</param>
    public void GreedyAlgo(Bag bag)
    {
        int idx;
        int ntc = 0;

        //重复选择
        while ((idx = ChooseFunc(bag, bag.totalC - ntc)) != -1)
        {
            //所选物品是否满足背包承重要求?
            if (ntc + bag.list[idx].weight <= bag.totalC)
            {
                bag.list[idx].status = 1;
                ntc += bag.list[idx].weight;
            }
            else
            {
                //不能选这个物品了，做个标记后重新选
                bag.list[idx].status = 2;
            }
        }

        PrintResult(bag);
    }

    /// <summary>
    /// 策略函数——实现选择策略
    /// 从剩余物品中选择价值最大的
    /// </summary>
    /// <param name="list">背包</param>
    /// <param name="C">背包剩余重量</param>
    private int ChooseFunc(Bag bag, int C)
    {
        int index = -1;
        int mp = 0;
        for (int i = 0; i < bag.list.Count; i++)
        {
            Item item = bag.list[i];
            if (item.status == 0 && item.price > mp)
            {
                mp = item.price;
                index = i;
            }
        }
        return index;
    }

    /// <summary>
    /// 打印结果
    /// </summary>
    /// <param name="bag"></param>
    private void PrintResult(Bag bag)
    {
        int totalPrice = 0;
        int totalC = 0;

        Console.Write("选择结果为: ");
        for (int i = 0; i < bag.list.Count; i++ )
        {
            if (bag.list[i].status == 1)
            {
                totalPrice += bag.list[i].price;
                totalC += bag.list[i].weight;

                Console.Write(i+ " ");
            }
        }
        Console.WriteLine();
        Console.WriteLine("总重量: "+totalC);
        Console.WriteLine("总价格: "+totalPrice);
    }
}

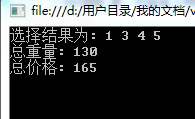
运行效果: