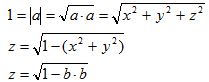通常将只有大小的量(如物体的质量、体积、密度等)统称为标题或数量，而将既有大小，又有方向的量(如速度、加速度等)统称为矢量或向量。

设有向量a(x1,y1,z1), b(x2,y2,z2), 有关的向量运算有:

(1)向量的长度

(2)两个向量的和差运算

(3)两个向量的点乘运算

(4)两个向量的叉乘积

(5)设a=(x,y,z)、b=(x,y)，且a为单位向量，当z>0时，则可通过x、y推导出z值。

柯西-施瓦茨不等式

$$-|\boldsymbol{a}||\boldsymbol{b}|≤|\boldsymbol{a}||\boldsymbol{b}|cosθ≤|\boldsymbol{a}||\boldsymbol{b}|$$

证明 根据余弦函数的性质，对任意的θ，有 -1≤cosθ≤1, 两边同时乘以 |a||b|，有 $$-|\boldsymbol{a}||\boldsymbol{b}|≤|\boldsymbol{a}||\boldsymbol{b}|cosθ≤|\boldsymbol{a}||\boldsymbol{b}|$$ 利用定义式 a●b=|a||b|cosθ，可得。

根据柯西-施瓦茨不等式，可以得出以下事实:
① 当两个向量方向相反时，内积取得最小值。
② 当两个向量不平行时，内积取平行时的中间值。
③ 当两个向量方向相同时，内积取得最大值。