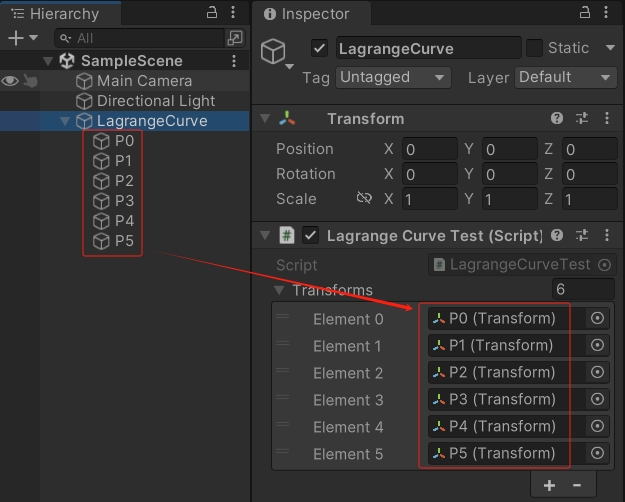
一、工程截图

二、插值脚本

using UnityEngine;
/// <summary>
/// 拉格朗日曲线插值类
/// </summary>
public sealed class LagrangeCurve
{
    /// <summary>
    /// 拉格朗日曲线插值算法
    /// </summary>
    /// <param name="points">型值点</param>
    /// <param name="t">插值参数，取值范围[0,1]</param>
    /// <returns></returns>
    public static Vector3 Lerp(Vector3[] points, float t)
    {
        //--参数有效性检测--
        if (t < 0) t = 0;
        if (t > 1) t = 1;

        if (points == null || points.Length == 0)
            return Vector3.zero;
        if (points.Length == 1)
            return points[0];
        //--End--

        //直接返回起始点
        if (t <= 0)
            return points[0];
        //直接返回终点
        if (t >= 1)
            return points[points.Length-1];

        Vector3 result = Vector3.zero;

        //路径总长度
        float s = 0;
        //存放每个型值点所在位置的路径长度
        float[] lengths = new float[points.Length];
        lengths[0] = 0;
        for (int i = 1; i < points.Length; i++)
        {
            float d = Vector3.Distance(points[i - 1], points[i]);
            s += d;
            lengths[i] = s;
        }
        //计算线性插值距离
        float l = s * t;
        //临时变量
        float x=0, y=0, z=0;
        int count = points.Length;
        //算法实现
        for (int i = 0; i < count; i++)
        {
            Vector3 p = points[i];
            x = p.x;
            y = p.y;
            z = p.z;
            //型值点的值与混合函数值相乘
            for (int j = 0; j < count; j++)
            {
                if (i == j)
                    continue;
                float ti = lengths[i];
                float tj = lengths[j];
                t = (l - tj) / (ti - tj);
                x *= t;
                y *= t;
                z *= t;
            }
            //线性组合
            result.x += x;
            result.y += y;
            result.z += z;
        }
        return result;
    }
}

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class LagrangeCurveTest : MonoBehaviour
{
    [SerializeField]
    private List<Transform> transforms = new List<Transform>();
    private Vector3[] points;

    private void Update()
    {
        points = new Vector3[transforms.Count];
        for (int i = 0; i < transforms.Count; i++)
        {
            points[i] = transforms[i].position;
        }

        float step = 0.01f;
        float t = 0f;
        while(t < 1)
        {
            Vector3 v0 = LagrangeCurve.Lerp(points, t);
            t += step;
            Vector3 v1 = LagrangeCurve.Lerp(points, t);
            Debug.DrawLine(v0, v1, Color.red);
        }
    }
}

运行测试