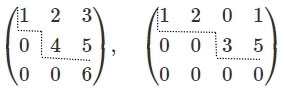线性代数主要处理与数量的线性关系相关的问题，和其他数学课程一样，线性代数有两类基本的数学构件：一类是对象、数据；一类是这些对象进行的运算，本章就是讨论最简单的由数形成的矩形数表——矩阵及其运算，矩阵是线性代数的一个最基本的概念。矩阵的运算是线性代数的基本内容。在数学科学、自然科学、工程技术与生产实践中，有许多问题都可以归结为矩阵的运算，进而用矩阵的理论来处理。

  本章首先介绍矩阵的概念，然后介绍矩阵的线性运算、乘法、转置、可逆矩阵、矩阵的初等变换、分块矩阵以及方阵的行列式和矩阵的秩.

» 矩阵的基本概念

在现实生活中，人们往往不仅需要使用单个的数，而且还要处理成批的数。这就需要把数的概念推广到矩阵。

定义 1.1 由m×n个数$a_{ij}(i=1,2,\cdots,m;\; j=1,2,\cdots,n)$按一定的次序排成m行n列的表 $$ A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \quad & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} $$ 称为一个m行n列的矩阵。横的每排叫做矩阵的行，纵的每排叫做矩阵的列。$a_{ij}$叫做矩阵A的第i行，第j列的元素。i和j分别叫做$a_{ij}$的行指标和列指标。矩阵A又可记作$(a_{ij})$，$(a_{ij})_{m×n}$或$A_{m×n}$。通常用大写英文字母A，B，C，$\cdots$来表示矩阵。

例如变量$x_1,x_2$与$y_1,y_2,y_3$的关系式 $$ \left\{ \begin{aligned} x_1=a_{11}y_1+a_{12}y_2+a_{13}y_3 \\ x_2=a_{21}y_1+a_{22}y_2+a_{23}y_3 \end{aligned} \right. $$ 中的系数就构成一个矩阵 $$ A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ \end{pmatrix} $$

元素都是实数的矩阵称为实矩阵，元素都是复数的矩阵称为复矩阵.

当一个矩阵的行数与列数都是n时，称该矩阵为n阶方阵或n阶矩阵。在n阶矩阵A中，元素$a_{ij}(i=1,2,\cdots,n)$排成的对角线称为方阵的主对角线。

一个m行1列的矩阵 $$ A_{m×1}=\begin{pmatrix} a_{11} \\ \vdots \\ a_{m1} \end{pmatrix} $$ 称为一个列矩阵或列向量。我们常用希腊字母$α,β,γ,\cdots$表示列向量。

类似地，一个1行n列的矩阵 $$ A_{1×n}=(a_{11} \quad \cdots \quad a_{1n}) $$ 称为一个行矩阵或行向量。为了醒目起见，我们通常在行向量的元素之间加上逗号，即$A_{1×n}=(a_{11},\cdots,a_{1n})$。

特别地，一个1×1的矩阵$(a_{11})$就是一个数，此时可以将括号去掉，直接记成$a_{11}$。这就是说，数可看成矩阵的特例。

» 几种特殊的矩阵

在利用矩阵解决问题时，经常遇到下面几种特殊矩阵。

零矩阵：若一个矩阵的所有元素均为零，则这个矩阵称为零矩阵，记为O。

对角矩阵：若一个n阶矩阵除主对角线上的元素之外，其余元素全部为零，则称此矩阵为对角矩阵，通常用Λ表示，即 $$ \Lambda = \begin{pmatrix} a_{11} & \quad & \quad & \quad \\ \quad & a_{22} & \quad & \quad \\ \quad & \quad & \ddots & \quad \\ \quad & \quad & \quad & a_{nn} \\ \end{pmatrix} $$ 这里非主对角线上的元素0可以省略不写，或记为Λ=diag$(a_{11},a_{22},\cdots,a_{nn})$。

数量矩阵：若对角矩阵Λ的主对角线上的元素为同一个数a，即$a_{11}=a_{22}=\cdots=a_{nn}=a$，则称此矩阵为数量矩阵。

单位矩阵：若n阶数量矩阵的主对角线上的元素为1，则此矩阵称为单位矩阵，记为E或E_n，即 $$ E = \begin{pmatrix} 1 & \quad & \quad & \quad \\ \quad & 1 & \quad & \quad \\ \quad & \quad & \ddots & \quad \\ \quad & \quad & \quad & 1 \\ \end{pmatrix} $$

三角矩阵：若一个方阵的主对角线下(上)面的元素全为零，则此矩阵称为上(下)三角矩阵。上、下三角矩阵统称为三角矩阵。

行阶梯形矩阵：若一个矩阵$A=(a_{ij})m×n$中的某一行元素全为零，则称这一行为零行，否则称之为非零行。非零行的第一个非零元素称为非零首元。若A的各非零行的非零首元的列指标随着行指标的增大而严格增大，并且零行（如果有的话）均在所有非零行的下方，则此矩阵称为行阶梯形矩阵。例如

行最简形矩阵：若一个行阶梯形矩阵的每个非零行的非零首元均为1，并且此非零首元所在列的其余元素均为零，则此矩阵称为行最简形矩阵。例如 $$ \begin{pmatrix} 1 & -1 & 0 & 1 \\ 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} $$ 是行最简形矩阵。