1、计算点到平面的距离

设想一个平面和一个不在平面上的点q。平面上存在一个点p，它到q的距离最短。很明显，从p到q的向量垂直于平面，且形式为an。如下图所示。

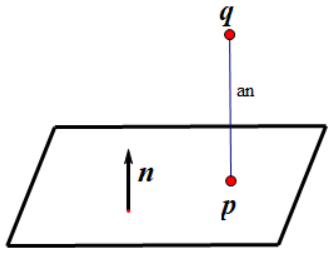
假设n为单位向量，那么p到q的距离（也就是q到平面的距离）就是a了。（如果q在平面的反面，这个距离为负。）令人惊奇的是，不用知道p的位置就能计算出a。让我们回顾下q的原定义，并做一些向量计算以消掉p。

计算任意点到平面的有符号距离公式 \begin{flalign} &\mathbf{p}+a\mathbf{n}=\mathbf{q} &\\ &(\mathbf{p}+a\mathbf{n})\cdot \mathbf{n}=\mathbf{q}\cdot \mathbf{n} &\\ &\mathbf{p}\cdot\mathbf{n}+(a\mathbf{n})\cdot\mathbf{n}=\mathbf{q}\cdot\mathbf{n} & \\ &d+a=\mathbf{q}\cdot\mathbf{n} &\\ &a=\mathbf{q}\cdot\mathbf{n}-d \end{flalign} $d=\mathbf{p}\cdot\mathbf{n}$为p向量在n(法向量)上的投影距离。因为在平面上任选一点p，它在n上的投影距离都是相等的。所以公式中的p点可以在平面上任意选择。