点光源和力学中的质点类似，只要当用来测定光的辐射的某个位置，其与光源的距离是光源的最大尺寸的某倍时，该光源就可以被视为点光源，通常该倍数不小于15。点光源以球面波的方式向空间辐射电磁波。如果在传输介质中没有反射、散射和吸收，那么在给定方向上的某一个立体角内，无论辐射距离有多远，其辐射能量是不变的。

  辐射强度(radiation intensity)定义为在给定传输方向上，单位立体角内光源发出的辐射通量。令辐射通量为Φ，立体角为Ω，辐射强度为I，则以微分形式定义光的辐射强度公式如下：

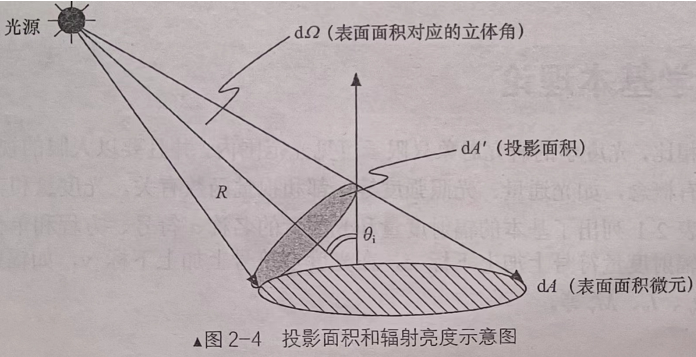
$$ I=\frac{dΦ}{dΩ} $$

  辐射亮度(radiance)定义为辐射表面在其单位投影面积的单位立体角内发出的辐射能量。如图所示：

  上图中，在待考察的辐射表面中，取表面面积微元dA进行讨论，光线穿过面积微元dA与面积微元的法线夹角为θ_i，则面积微元的投影面积dA'=dAcosθ，然后将dAcosθ视为一个正圆锥体（应用极限的观念看待一个面积微元收缩成一个“点”的做法），乘以一个立体角值（单位是球面度），便得到立体角所截的球面面积dAcosθdΩ。令辐射亮度为L，则辐射亮度的微分定义如下：

$$ L=\frac{d^2Φ}{dΩdAcosθ}=\frac{dI}{dAcosθ} $$

$d^2Φ$表示辐射通量的二阶微分形式。

  辐射亮度描述光源的面积微元在垂直传输方向上的辐射强度特性。例如，描述一个白炽灯时，描述白炽灯每一局部表面的发射特性通常没有实际意义的；而把它视为一个点光源时，就可以描述在某个给定观察方向上的辐射强度。

辐射出射度和辐射入射度

  辐射出射度(radiant exitance)定义为离开光源表面的单位面积的辐射通量，令辐射出射度为M，则以微分形式定义辐射出射度的公式为：

$$ M=\frac{dΦ}{dA} $$

  面积微元对应的立体角是光源辐射的整个半球空间（注意是半球而不是整个球）。例如，太阳表面的辐射出射度指太阳的单位表面积向外部空间发射的辐射通量。

  辐射入射度(irradiance，以译为“辐照度”)定义为单位面积被照射的辐射通量，令辐射入射度为E，则以微分形式定义辐射入射度的公式为：

$$ E=\frac{dΦ}{dA} $$

  由上式可以推得：对于点光源，给定辐射通量为Φ，则它在一个半径为R的球面某一面积微元上的辐射入射度遵循距离平方反比定律，如下所示：

$$ E=\frac{Φ}{4πR^2} $$

  辐射入射度和辐射出射度的定义方程和单位是相同的，分别用来描述面积微元发射和接受辐射通量的特性。如果一个表面能反射出入射至其表面的全部辐射通量，那么该表面可以视为一个辐射源表面。辐射度相关的物理量可以视为电磁波波长的函数。因此，在描述辐射度相关的物理量时，可以在相应的名称加上波长符号λ，写成函数形式，如辐射通量Φ可以记为Φ(λ)。辐射入射度和辐射出射度的概念和基于物理的渲染模型有直接关系。