这个网站提供了大量颜色空间理论的相关资料：http://www.brucelindbloom.com/index.html

  因为人眼中有3种感知色彩的视锥细胞，所以理论上用3种不同颜色的光就可以混合出自然界中任何一种颜色来。人们通过大量的实验，通过对3种颜色的光源进行匹配，得到了人眼对于不同颜色光的匹配函数。

  这一类实验的过程大致如下：把一个银幕用不透光的挡板分割成两个区域，用一束待测试颜色的光线照射左区域，待测试颜色记为C（以下用大写字母表明颜色，用小写字母表明分量大小）。同时用3种不同颜色的光同时照射右区域，这3种不同颜色的光称为源颜色光，记为C₁、C₂、C₃。然后调节3种源颜色光的强度，直到银幕左右两边区域上的颜色看上去一样为止。假设此3种源颜色光的强度分别为r₁、r₂、r₃，根据格拉斯曼定律所揭示的叠加性性质，有以下公式。

$$ C=i_1C_1+i_2C_2+i_3C_3 \tag{1} $$

  从实践中可知，在可视光范围内，任何一种波长的光刺激视锥细胞所产生的颜色感觉，可以经由最多3种精心选择的波长的光混合而成的“混合光”等价刺激而成。例如，某种波长让人生成“黄色”感觉的光，可以由两种分别让人生成“红色”和“绿色”感觉的不同波长的光混合刺激而成。任何一种“目标颜色”，由最多3种“基准颜色”按一定比例叠加而成，这就是公式(1)所描述的三色加法模型。

  根据上面的理论，只需要选定三原色且对其进行量化，就可以将颜色量化为数字信号。在三色加法模型中，如果某一种目标颜色C和另外一种三原色混合色C_mix给人的感觉相同时，三原色混合色中的3种基准颜色的份量就称为该目标颜色C的三色刺激值。对于如何选定三原色及对其量化，如何确定刺激值等问题。国际照明委员会于1931年定义了一套标准：CIE1931-RGB标准色度系数。

  CIE1931-RGB颜色模型分别选择了波长为700nm、546nm、436nm的这3种波长的光，作为产生三原色的基准，这3种光可称为三原色基准光，它们刺激光锥细胞，可以分别让人感觉到红、绿、蓝3原色。这3种波长的光可以由汞弧光谱滤波精确且稳定地产生出来。

  假设某个波长为λ的目标光，对应生成目标颜色C。依据普朗克公式，可以把该目标光的能量视为波长为λ的函数，写为E_C(λ)，则目标光的能量应为三原色基准光各自的能量乘以系数后之和。如果把三原色基准光各自的能量写成目标光波长λ的函数，并且称这些函数为颜色匹配函数（color matching function），则有E_R(λ)、E_G(λ)、E_B(λ)，如下式所示。

$$ \begin{equation} \left\{ \begin{aligned} E_R(λ)=δ(λ-λ_R), \quad λ_R=700nm \\ E_G(λ)=δ(λ-λ_G), \quad λ_G=546nm \\ E_B(λ)=δ(λ-λ_B), \quad λ_B=436nm \end{aligned} \right. \end{equation} \tag{2} $$

最终E_C(λ)可以写为

$$ E_C(λ)=α_{_R}E_R(λ)+α_{_B}E_B(λ)+α_{_G}E_G(λ) \tag{3} $$

公式(3)实质上就是用波长及能量的形式，对公式(1)进行改写。α_R、α_G、α_B则分别对应于三原色基准光各自的光亮度值。可以理解为在定义一个RGB颜色值时，R分量、G分量、B分量各占多少。如果直接用RGB的方式描述，公式(1)和公式(3)都可以改写成如下形式：

$$ C=rR+gG+bB \tag{4} $$

式中。C为目标光的颜色；R、G、B对应于红、绿、蓝3种基准光；r、g、b为混合产生目标光时需要3种基准光的强度，其取值范围在0~1。

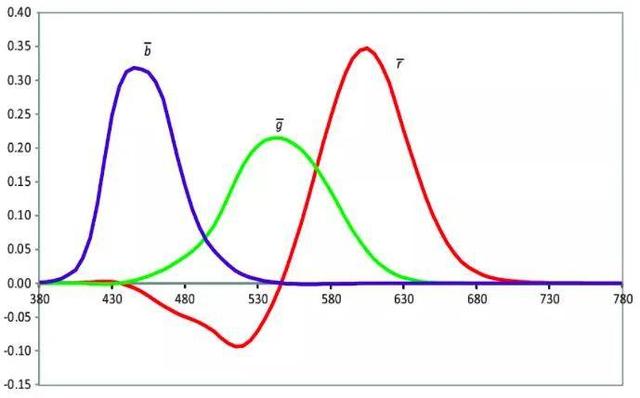
如果把r、g、b这些值视为坐标系的纵坐标，光的波长视为横坐标，则下图表示它们之间的关系：

上图中红色曲线出现了负值，是因为部分颜色，需要负强度的红色光源才能调节出来。而自然界中不可能有“负强度”的光。(这也是RGB模型的缺点)

相对权因子

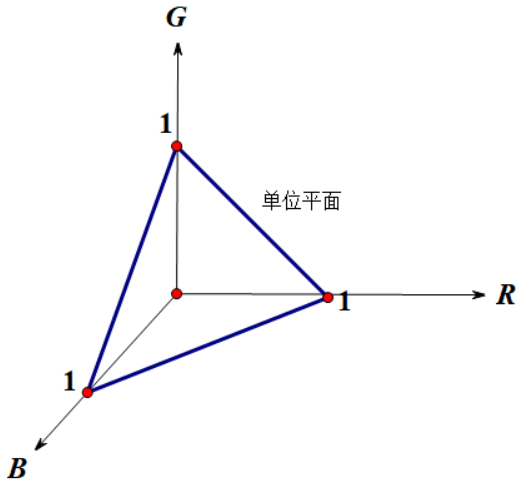
  根据用三原色基准光组合成一个任意颜色光的这一特性，可以沿着正交坐标轴画出每个基准光的值，所形成的空间可以称为三原色基准空间。任意颜色均可以由这个三原色基准空间中的一个矢量表示，即以坐标系原点为起点，分量为rR、gG和bB的矢量。矢量与单位平面的交点代表为获得颜色所需要的相对权因子，相对权因子又称为色度值或者色度坐标。

$$ \overline{r}=\frac{r}{r+g+b},\quad \overline{g}=\frac{g}{r+g+b},\quad \overline{b}=\frac{b}{r+g+b} \\ $$

式中，$\overline{r}+\overline{g}+\overline{b}=1$。

单位平面与色度图

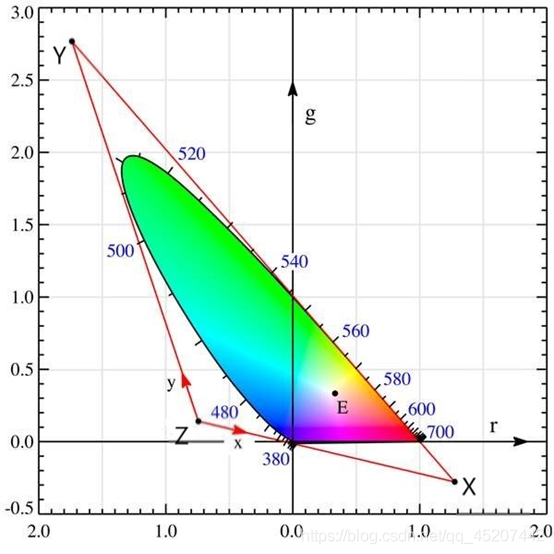
  单位平面在坐标平面上的投影产生色度图。色度图直接给出了r、g两种基准光颜色之间的函数关系，并且间接地给出与第三基准光颜色的关系，如$\overline{b}=1-\overline{r}-\overline{g}$。

  色度图中，边缘的曲线表示单色的光谱。例如，波长为540nm的单色光，由r=0、g=1、b=1-r-g=0三个基准光颜色的分量组成。再如，380~540nm波段的单色光，由于红色光分量存在负值(参见上面r(λ)曲线图),因此该段色域落在了r轴的负区间内。自然界中，人眼可分辨的颜色都落在光谱曲线包围的范围内。

  CIE1931-RGB颜色模型是根据实验结果制定的，出现的负值使得计算和转换时非常不方便。所以，国际照明委员会提出了一个假想模型，该模型假定人对色彩的感知是线性的（实际上并不是线性的）。该模型对CIE1931-RGB系统色度图进行了线性变换，将可见光色域变换到正数区域内。其方法是首先在CIE1931-RGB系统中选择了一个三角形，该三角形覆盖了所有可见光的色度，之后将该三角形进行如下式所示的线性变换，将可见色域变换到（0, 0）、（0, 1）及（1, 0）构成的正数区域内。也就是说，假想出3个不存在于自然界，但较之基准光RGB更方便计算的基准光XYZ，构成一个新的CIE1931-XYZ模型。

$$ \left[ \begin{array}{l} X \\ Y \\ Z \end{array} \right] = \frac{1}{b_{21}} \left[ \begin{array}{l} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array} \right] \left[ \begin{array}{l} R \\ G \\ B \end{array} \right] => \frac{1}{0.17697} \left[ \begin{array}{l} 0.49000 & 0.3100 & 0.20000 \\ 0.17697 & 0.8124 & 0.01063 \\ 0.00000 & 0.0100 & 0.99000 \end{array} \right] \left[ \begin{array}{l} R \\ G \\ B \end{array} \right] $$

颜色空间变换矩阵