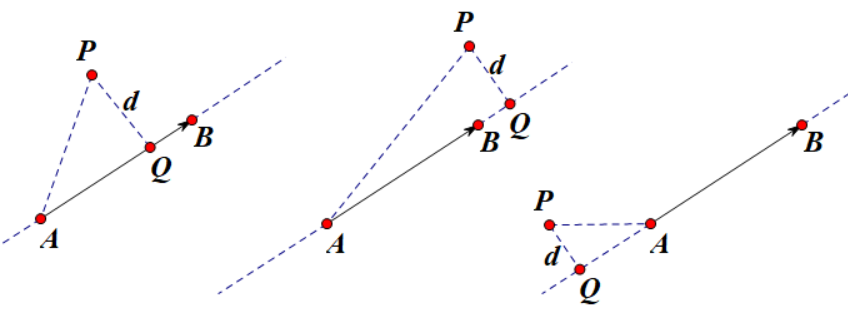
点P在向量AB上的投影为点Q，如果Q落在向量AB上，则PQ的长度即为点P到线段AB的距离。如果点Q落在向量AB之外，则点P到线段最近端的距离则为点P到线段AB的距离。

$ \overrightarrow{AP} \cdot \overrightarrow{AB}=|\overrightarrow{AP}||\overrightarrow{AB}|cosθ=|\overrightarrow{AP}||\overrightarrow{AB}|\frac{|\overrightarrow{AQ}|}{|\overrightarrow{AP}|}=|\overrightarrow{AQ}||\overrightarrow{AB}| $
$ |\overrightarrow{AQ}|=\frac{\overrightarrow{AP} \cdot \overrightarrow{AB}}{|\overrightarrow{AB}|} $
$ \overrightarrow{AQ}=|\overrightarrow{AQ}|\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} $
$ \overrightarrow{PQ}=\overrightarrow{AQ}-\overrightarrow{AP} $

(1) 当点Q落在向量AB上时

$|\overrightarrow{PQ}|$即为点P到线段AB的距离。

(2) 当点Q落在线段AB的延长线上时

如果$|\overrightarrow{AQ}|>|\overrightarrow{AB}|$，则说明点Q落在AB的延长线上。点P到线段AB的距离为$|\overrightarrow{PB}|$
如果$|\overrightarrow{AQ}|<0 \quad (即\overrightarrow{AP}与\overrightarrow{AB}的夹角为钝角)$，则说明点Q落在BA的延长线上。点P到线段AB的距离为$|\overrightarrow{PA}|$

也可以通过向量点乘判断
如果$\overrightarrow{AB} \cdot \overrightarrow{AP} < 0$，则点Q落在BA的延长线上。
如果$\overrightarrow{AB} \cdot \overrightarrow{AP} = 0$，则点Q与点A重合。
如果$\overrightarrow{BA} \cdot \overrightarrow{BP} < 0$，则点Q落在AB的延长线上。
如果$\overrightarrow{BA} \cdot \overrightarrow{BP} = 0$，则点Q与点B重合