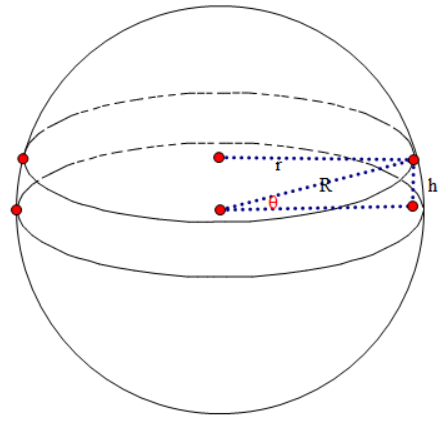
设：球的体积V，半径R，将球划分成n个圆柱体，每个圆柱体的半径为r，高为h(微元d_h)，底面积为s，体积为v，有

$ \begin{flalign} &h=R\cdot{sinθ} \\ &r=R\cdot{cosθ} \\ &s=πr^2 \\ &v=s×h=πr^2×R\cdot{sinθ}=π{(R\cdot{cosθ})^2}×R\cdot{sinθ} \end{flalign} $
$ \begin{flalign} V&=2\int_{0}^{R}sd_h=2\int_{0}^{R}πr^2d_h=2\int_{0}^{π/2}π(R\cdot{cosθ})^2d_{(R\cdot{sinθ})} \\ &=2πR^3\int_{0}^{π/2}cos^2θd_{sinθ}\\ &=2πR^3\int_{0}^{π/2}(1-sin^2θ)d_{sinθ}\\ &=2πR^3\left(\int_{0}^{π/2}d_{sinθ}-\int_{0}^{π/2}sin^2θd_{sinθ}\right)\\ &=2πR^3\left[sinθ-\frac{1}{3}sin^3θ\right]_{0}^{π/2} \\ &=2πR^3(1-\frac{1}{3})\\ &=\frac{4}{3}πR^3 \end{flalign} $