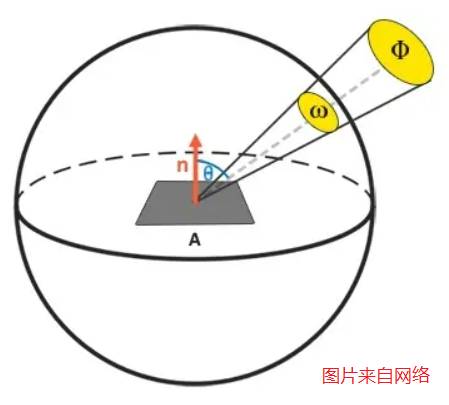
立体角

  给定一个正球体，它的半径为R。然后给定一个正圆锥体，正圆锥体的顶点和球心重合。圆锥体顶点到圆锥底面圆边上任意一点的连线，即正圆锥体斜高，它的值也为R。由正圆锥体的底面圆S所截取的那一部分球的面积A和球体半径R的平方的比称为立体角(solid angle)，其国际单位是球面度(steradian)。

若以Ω表示立体角，则立体角的微分形式定义如下式所示。 $$ dΩ=\frac{dA}{R^2} $$ 式中，dA为圆锥体底面截取的球面A的微元。

若在球面坐标系下对立体角进行定义，如上面右图所示，面积微元dA的高为$Rdθ$，宽为$Rsinθd\varphi$，那么面积微元dA的公式可以写为 $$ dA=RdθRsinθd\varphi $$ 那么由上式，整个球面的立体角可写为关于$\varphi$和θ的二重积分形式： $$ Ω=\int{\frac{dA}{R^2}}=\int\int{dθd\varphi sin\varphi}=\int^{2\pi}_0 d\varphi \int^\pi_0 sinθdθ=4\pi $$

更简单的理解，整个球的表面积为$4\pi r^2$，根据立体角的定义，可得整个球的立体角为: $$Ω=\frac{4\pi r^2}{r^2}=4\pi$$ 即，整个球空间有$4\pi$个球面度。

$\varphi$读作$|f\grave{a}i|$