卷积神经网络的特征映射的值以图像和过滤器的相似度作为输入信息。相似度可以利用下面的定理进行计算。

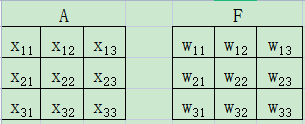
由3×3像素构成的两个数组A、F如下图所示。A、F的相似度可以像下面这样求出。 $$相似度=w_{11}x_{11}+w_{12}x_{12}+w_{13}x_{13}+\cdots+w_{33}x_{33}\tag{1}$$

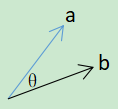
这个定理可以利用向量的性质来说明。当两个向量a、b相似时，它们的内积a•b较大。我们可以认为内积a•b的大小表示两个向量的相似性。 $$\boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|cosθ\quad (θ为两个向量的夹角)$$

两个向量的内积是它们的箭头长度乘以夹角的余弦。夹角越接近0，余弦的值越大。也就是说，当向量相似时，内积的值较大。

为了利用这个性质，我们将A、F看作以下向量。 $$ \begin{aligned} A&=(x_{11},x_{12},x_{13},x_{21},x_{22},x_{23},x_{31},x_{32},x_{33}) \\ F&=(w_{11},w_{12},w_{13},w_{21},w_{22},w_{23},w_{31},w_{32},w_{33}) \end{aligned} $$ 这样一来，两个向量的内积A•F就与上述的式(1)的右边一致了。也就是说，我们可以把式(1)解释为相似度。