应用数学最重要的任务之一就是寻找函数取最小值的点。梯度下降法是神经网络中找函数最小值的点的方法。在数值分析领域,梯度下降法也称为最速下降法。
通过导数找函数最小值
例 1 已知函数 z=f(x,y),求使函数取得最小值的 x、y ?
解 分别对x、y求偏导数,当x、y的偏导数都为0时,函数 z=f(x,y) 取得最小值。
$$\frac{\partial{f(x,y)}}{\partial{x}}=0,\quad\frac{\partial{f(x,y)}}{\partial{y}}=0$$
上式表明,与函数相切的平面变得水平时,那个切点即为函数的最小值点。
注意 上式只是寻找最小值点的必要条件,对于有多个极值点的函数要小心处理。
在神经网络中变量非常多,通常不采用联立偏导方程组求解。
梯度下降法的基本思路
先在函数上随便取一个点,然后向最陡的方向移动一小段距离,再次判断最陡的方向,然后再向最陡的方向移动一小段距离,不断重复这种操作,便可沿最短路径到达函数底部(最小值点)。
例 2 函数z=f(x,y)中,当x改变△x,y改变△y时,函数f(x,y)的值的变化△z?
解 根据近似公式,以下关系式成立。 $$\Delta{z}=f(x+\Delta{x},y+\Delta{y})-f(x,y)=\frac{\partial{f(x,y)}}{\partial{x}}\Delta{x}+\frac{\partial{f(x,y)}}{\partial{y}}\Delta{y}$$ 可以将上式表示为两个向量的内积形式 $$\left(\frac{\partial{f(x,y)}}{\partial{x}},\frac{\partial{f(x,y)}}{\partial{y}}\right),\quad(\Delta{x},\Delta{y})$$ 当两个向量的方向相反时,这两个向量的内积取得最小值,根据向量的这条性质得 $$(\Delta{x},\Delta{y})=-η\left(\frac{\partial{f(x,y)}}{\partial{x}},\frac{\partial{f(x,y)}}{\partial{y}}\right)\quad(η为正的微小常数)$$ 注:希腊字母η读作ita
向量$(\Delta{x},\Delta{y})$称为位移向量。向量$\left(\frac{\partial{f(x,y)}}{\partial{x}},\frac{\partial{f(x,y)}}{\partial{y}}\right)$称为函数f(x,y)在点(x,y)处的梯度(gradient)。梯度给出了最陡的坡度方向。
将上面的公式推广到n个变量 $$(\Delta{x_1},\Delta{x_2},\cdots,\Delta{x_n})=-η\left(\frac{\partial{f}}{\partial{x_1}},\frac{\partial{f}}{\partial{x_2}},\cdots,\frac{\partial{f}}{\partial{x_n}}\right)$$ 神经网络中会涉及到成千上万个变量,用上面的式子表示就显得十分冗长。
更简洁的表达式 $$ \begin{aligned} \Delta{x}&=(\Delta{x_1},\Delta{x_2},\cdots,\Delta{x_n})\\ \nabla{f}&=\left(\frac{\partial{f}}{\partial{x_1}},\frac{\partial{f}}{\partial{x_2}},\cdots,\frac{\partial{f}}{\partial{x_n}}\right) \end{aligned} $$ $\nabla$在向量分析领域,称为哈密顿算子。
注:希腊字母$\nabla$读作nabla
利用上面的$\Delta{x}$和$\nabla{f}$,梯度下降法的基本公式可以简洁地表示为 $$\Delta{x}=-η\nabla{f}$$
η可以看作移动的“步长”,根据η的值,可以确定下一步移动到哪个点。如果步长较大,那么可能会到达最小值点,也可能会直接跨过了最小值点(左图)。而如果步长较小,则可能会滞留在极小值点(右图)。
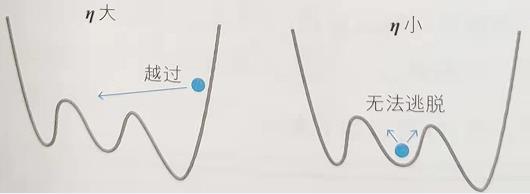
在神经网络中,η称为学习率。遗憾的是,它的确定方法没有明确的标准,只能通过反复试验来寻找恰当的值。
η与步长
上面的讨论是将η看作步长,实际上这并不正确,正确的做法应该是将整个右侧看作步长$-η\left(\frac{\partial{f}}{\partial{x_1}},\frac{\partial{f}}{\partial{x_2}},\cdots,\frac{\partial{f}}{\partial{x_n}}\right)$,为了让“步长”均匀,需要将梯度修正为单位向量,如下: $$(\Delta{x},\Delta{y})=-η\left(\frac{\partial{f(x,y)}}{\partial{x}},\frac{\partial{f(x,y)}}{\partial{y}}\right)\biggl{/}\sqrt{ \left(\frac{\partial{f(x,y)}}{\partial{x}}\right)^2+\left(\frac{\partial{f(x,y)}}{\partial{y}}\right)^2}$$ 经过以上修正后,就可以将η看作步长了。
单变量函数的梯度下降法
梯度下降法也可以用于单变量函数,将偏导数替换为导数,将得到的下式作为梯度下降法的基本公式。 $$\Delta{x}=-ηf'(x)\quad(η为正的微小常数)$$
验证梯度下降法
例 对于函数$z=x^2+y^2$,请用梯度下降法求出使函数取得最小值的x、y值
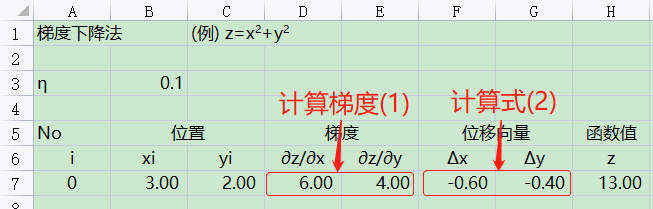
解 首先求出梯度 $$梯度\quad \left(\frac{\partial{z}}{\partial{x}}, \frac{\partial{z}}{\partial{y}}\right)=(2x, 2y)\tag{1}$$
接下来,逐步进行计算。
① 初始设定
随便给出初始位置$(x_i,y_i)(i=0)$与学习率η。
② 计算位移向量
对于当前位置$(x_i,y_i)$,算出梯度,然后根据梯度下降法的基本公式,求位移向量$\Delta{x}=(\Delta{x_i},\Delta{y_i})$,根据(1)式可得 $$(\Delta{x_i},\Delta{y_i})=-η(2x_i,2y_i)=(-η \cdot 2x_i,-η \cdot 2y_i)\tag{2}$$
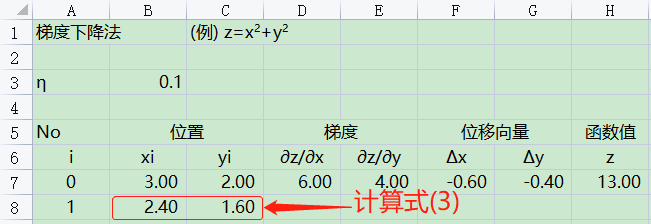
③ 更新位置
根据梯度下降法,由下式求出从当前位置$(x_i,y_i)$移动到点$(x_{i+1},y_{i+1})$。 $$(x_{i+1},y_{i+1})=(x_i,y_i)+(\Delta{x_i},\Delta{y_i})\tag{3}$$
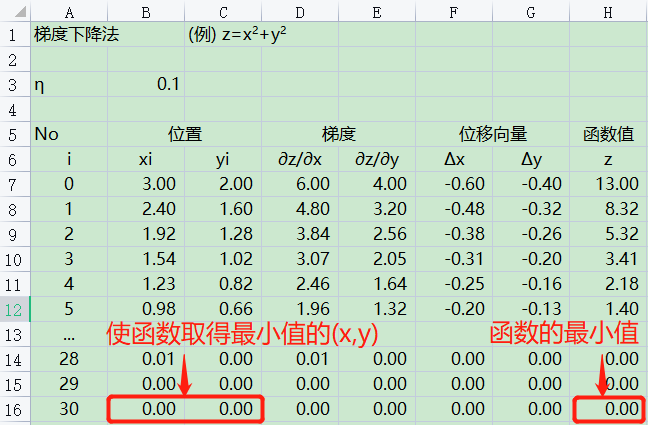
④ 反复执行②~③的操作
下图是反复执行②~③的操作30次后得出的坐标$(x_{30},y_{30})$的值。
与建立偏导方程组求解出的值一致。 $$偏导方程组\quad \begin{equation} \left\{ \begin{aligned} \frac{\partial{z}}{\partial{x}}=2x=0 \\ \frac{\partial{z}}{\partial{y}}=2y=0 \end{aligned} \right. \end{equation} $$ 解偏导方程组得,x=0,y=0