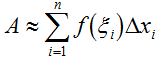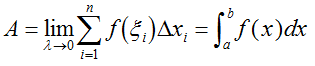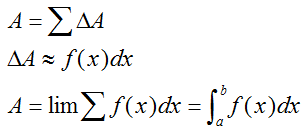在自然科学和生产实践中，有许多实际问题最后都能归结为定积分问题。本节将应用定积分的方法导出一些几何量与物理量的计算公式。但要强调的是，学习本节的目的并不只是记住这几个具体的公式，而是要通过这些实例了解并掌握定积分的微元分析法。

一、微元分析法

为了说明微元分析法的解题思路，让我们先复习一下曲边梯形面积问题的处理方法。

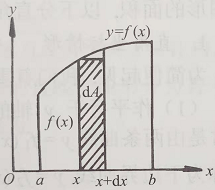
设函数f(x)在区间[a,b]上连续非负，将以曲线y=f(x)为顶边，底为[a,b]的曲边梯形的面积记为A，把A表示为定积分的步骤是：

(1) 分割
用任意一组分点把区间[a,b]分成长度为△x_i(i=1,2,...,n)的n个小区间，相应地把曲边梯形分成n个很窄的曲边梯形，第i个窄曲边梯形的面积设为△A_i，于是有

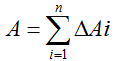
(2) 近似
将每一个窄曲边梯形近似为矩形，在其相应的小区间上任意取一点ξ_i，进而将函数值f(ξ_i)当做这个矩形的高，计算△A_i的近似值

(3) 求和
求和得A的近似值

(4) 取极限
取极限得

从上述步骤可以看出，能用定积分表示量A的前提是：量A(面积)与区间[a,b]有关，当区间[a,b]被任意分为若干个小段时，量A总是相应地被分为若干个部分量，且A等于所有部分量之和。这一性质称为量A对于区间[a,b]具有可加性。

把以上过程简述为 “化整为零” 与 “积零成整” 两个步骤。其中，“以直代曲” 或 “以不变代变” 是问题得以转化的关键，它要求近似式△A_i≈f(ξ_i)△x_i中当△x_i→0时，f(ξ_i)△x_i与△A_i之差(即，误差)是关于△x_i的高阶无穷小量(即，必须满足微分的定义)，这样才能保证的正确性。微分与导数的关系

为了简化起见，我们省略下标i，用△A表示任意一个小区间[x,x+dx]上的窄曲边梯形的面积，取[x,x+dx]的左端点x为ξ，从而

其中的f(x)dx称为面积微元，记为 dA=f(x)dx

一般情况下，若量I是非均匀地分布在某区间[a,b]上的整体量，且对区间[a,b]具有可加性，则可以按照下面的简化步骤把它表示为定积分。

(1) 求微元。将区间[a,b]任意分成n个小区间，再把量I相应地分为n个部分量，取其中任意一个小区间并记为[x,x+dx]，把相应于这个小区间的部分量△I近似地表示为[a,b]上的一个连续函数在点x处的值f(x)与△x的乘积，即△I≈f(x)△x，称f(x)dx为量I的微元,记为dI，即 dI=f(x)dx

(2) 作积分把这些微元无限相加，即以f(x)dx为被积式在区间[a,b]上作定积分，得

上述简化了步骤的方法通常称为定积分的微元法或元素法。这不是一个严密的数学定义，而只是应用定积分表示对区间[a,b]具有可加性的量的处理方法。

值得注意的是，△I与dI=f(x)dx的差必须是较△x高阶的无穷小。今后，我们往往模仿处理曲边梯形面积和变速直线运动的路程、变力沿直线作功等问题时所采用的“以不变代变”的方法，即在每一个小区间上将连续变量视为常量，就可保证所取的△I的近似值dI具有这样的性质。