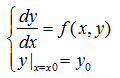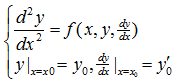函数是反映客观现实世界运动过程中量与量之间的一种关系，利用函数关系，可以对客观事物的运动规律进行研究。但是在大量的实际问题中遇到稍为复杂的一些运动时，反映运动规律的函数关系往往不能直接写出来，只能根据问题所提供的条件建立自变量、未知函数和未知函数的导数的关系式，这种含未知函数的导数的关系就称为微分方程，进一步对微分方程进行研究，解出未知函数，这就是所谓的解微分方程。

我们通过实例来引入微分方程的基本概念

例 1 一曲线通过点(1, 2)且在该曲线上任一点M(x,y)处的切线斜率为2x，求这条曲线的方程。

解 设所求曲线的方程为y=y(x)，根据导数的几何意义可知，曲线y=y(x)应满足关系式

这是一个含有未知函数y=y(x)的导数的方程，称为微分方程。未知函数y=y(x)还应满足下列条件：

y(1)=2

对微分方程两边进行积分，有

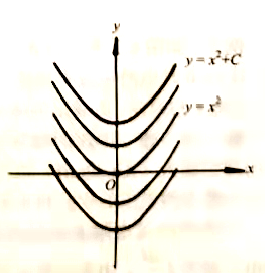
其中，C为任意常数，即满足微分方程的曲线有无穷多条，它们是一族抛物线。

又由于所求曲线过点(1,2)，所以有

求得C=1，于是所求曲线的方程为

定义1 含有未知函数的导数或微分的方程，称为微分方程。

如果微分方程中所含未知函数是一元函数，则称该微分方程为常微分方程；如果未知函数是多元函数，则称该微分方程为偏微分方程。

定义2 在微分方程中所出现的未知函数的导数或微分的最高阶数，称为该微分方程的阶数。

如果n阶微分方程具有形式为

则称该微分方程为n阶线性微分方程，其中a_i(x)(i=1,2,...,n)和f(x)都是x的已知函数。不是线性的微分方程，就称为非线性微分方程。

定义3 如果将一个函数y=y(x)代入微分方程后，能使微分方程两端成为恒等式，则称这个函数y=(x)为该微分方程的解。

例如，y=x^2+1是微分方程dy/dx=2x的解；对任意常数C，y=x^2+C也是微分方程dy/dx=2x的解。

定义4 若微分方程的解中所含相互独立的任意常数的个数等于该微分方程的阶数，则称该微分方程的通解（一阶微分方程通解含一个任意常数）；在通解中给任意常数以确定的值所得的解称为该微分方程的特解；确定特解的条件称为初始条件。

例如，s=1/2gt^2+C1t+C2是微分方程d^2s/dt^2=g的通解。而s=1/2gt^2+2C1+3C2和s=1/2gt^2+C1t都是微分方程d^2s/dt^2=g的解，但它不是微分方程d^2s/dt^2=g的通解。因为前者虽然含有两个任意常数，但它们不是独立的，只要令C=2C1+3C2就合并成为一个任意常数了，后者只含一个任意常数。而y=x^2+C是微分方程dy/dx=2x的通解。

例如，y=x^2+100是微分方程dy/dx=2x的一个特解。一般在确定了通解中的任意常数后，就能得到微分方程的特解，它可由初始条件y(0)=100来确定。

微分方程与初始条件一起称为初值问题。

一阶微分方程的初值问题

二阶微分方程的初值问题

n阶微分方程的通解含有n个独立的任意常数，其一般形式为：

其中C1，C2，...，Cn为相互独立的任意常数，若上式表示为

则称它为微分方程的显式解，否则称为微分方程的隐式解或通积分。