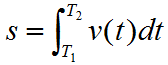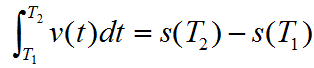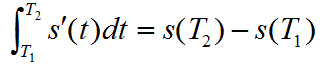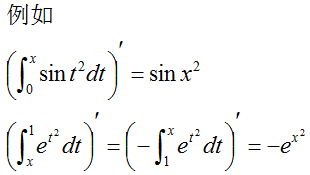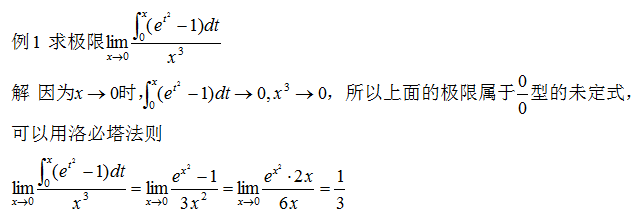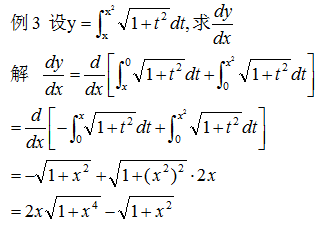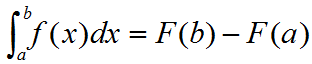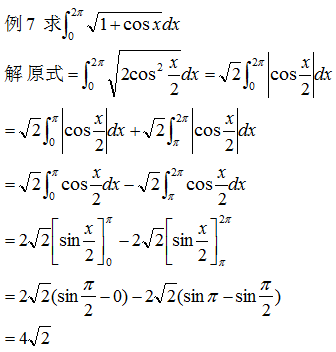在引进定积分的概念时，曾经讨论过变速直线运动的路程。若质点运动的速度为v(t)，则质点从时刻T1到T2所经过的路程为
另一方面，如果知道质点的运动规律（即位置函数）为 s=s(t) ，则质点从T1到T2所经过的路程为
从而有
由导数定义和 s`(t)=v(t)，即
这就是微积分基本公式。这一公式表明，要求定积分
，可以不再从定积分定义出发，而从速度函数（被积函数）v(t)，求路程函数 s(t) (被积函数的原函数)，然后计算 s(T2)-s(T1)
一、变上限定积分
设函数f(x)在区间[a, b]连续，并且x为区间[a, b]上任一点，显然f(x)也在[a, x]上连续，于是积分
一定存在，这是一个上限为变量的定积分。因为定积分的值与积分变量无关，为了区别积分上限和积分变量，不妨把积分变量改用其他字母，比如用t来表示，这样，上面的定积分就可以写成
.
当x在区间[a, b]上取定，就有一个确定的数值与之对应，所以该积分在区间[a, b]上定义了一个新的函数，称为积分上限的函数，记为Φ(x)，即
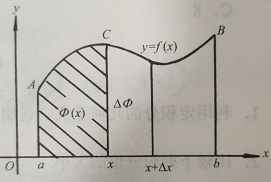
在几何上，若f(x)≥0，函数Φ(x)表示右侧竖边可以变动的曲边梯形AaxC的面积(如下图所示),这个面积随着右侧竖边的位置x的改变而改变，当x给定后，这条竖边的位置也就确定了，于是面积Φ(x)也随之确定，因而Φ(x)有时也称为面积函数。
对函数Φ(x)有下面的重要性质：
定理 1 （对积分上限的导数）设函数f(x)在区间[a, b]上连续，则对[a, b]上任一点x，积分上限的函数
的导数存在，且
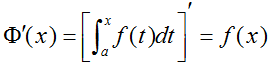
即对于变上限的定积分，对积分上限的导数等于被积函数在其上限处的值。
由原函数的定义，从定理1知Φ(x)是连续函数f(x)的一个原函数。因此，有下面的原函数的存在定理：
这个定理肯定了连续函数的原函数一定存在。同时，也初步揭示了定积分与原函数的关系。
二、牛顿(Newton)——莱布尼茨(Leibniz)公式
定理 3 如果函数F(x)是连续函数f(x)在区间[a, b]上的原函数，则
证 已知函数F(x)是连续函数f(x)的一个原函数，又由定理2知，积分上限的函数
也是f(x)的一个原函数，于是这两个函数之差必定等于某一个常数C0,即
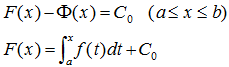
在上式中，令 x=a，注意到
，故得
因此
再令 x=b，代入得
这个公式称为牛顿——莱布尼茨公式，它是微积分学中的基本公式，通常将F(b)-F(a)记为
，即
这个公式告诉我们：要计算定积分
的 数值，只需要求出被积函数f(x)的一个原函数，然后计算这个原函数在积分上限的函数值与积分下限的函数值之差。这样，就把求定积分的问题转化为求被积函数f(x)的原函数的问题了。
读者应注意：由于 0≤x≤2π时，cos(π/2)不是非负的，因此
(不加绝对值符号就错了)，为了要计算积分
，必须先去掉被积函数的绝对值符号，因此，需将积分区间[0, 2π]分成两个区间[0, π]与[π, 2π]，再用对区间的可加性将所求积分表示成两个积分之和。
最后，我们指出，由微积分基本公式知道，微分与积分互为逆运算，有着密切的联系。因此，有关微分的定理、公式与法则，往往和有关积分的定理、公式与法则相互成对出现。