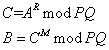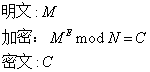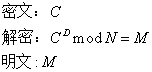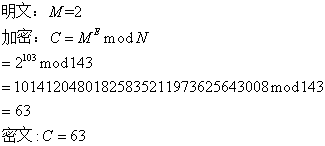RSA公钥加密算法是第一个既能用于数据加密也能用于数字签名的算法。

RSA定理

若P和Q是两个相异质数，另有正整数R和M，其中M的值与(P-1)(Q-1)的值互质，并使得(RM) mod (P-1)(Q-1) = 1。有正整数A，且A<PQ，设：

则有：A=B

1. 生成公钥PK和私钥SK的步骤:

(1) 随意选择两个大的素数P和Q，P不等于Q

(2) 将P、Q两个素数相乘得到一个数N，即 N=PQ

(3) 将P、Q分别减1，再相乘，得到一个数T，即 T=(P-1)(Q-1)

(4) 选择一个整数E，作为一个密钥，使E与T互质(即E与T的最大公约数为1)

(5) 根据公式 DE mod T = 1，计算出D的值，作为另一个密钥

(6) 通过以上步骤计算得出N、E、D这3个数据，其中(N、E)作为公钥，(N、D)作为私钥(当然也可以将公钥和私钥互换)

(7) 对外发布公钥

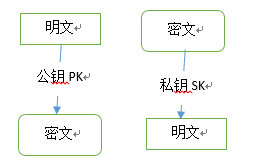
2. 用公钥加密信息

3. 用私钥解密信息

RSA算法实践

1. 生成公钥PK和私钥SK的过程如下：

取 P=11, Q=13

则 N=PQ=11x13=143

    T=(P-1)(Q-1)=10x12=120

取 E=7

由 DxE mod T=1

    Dx7 mod 120=1

得 D=103

则: 公钥(143, 7)，私钥(143, 103)

2. 用公钥加密

由于是手工计算，为了使计算的数据量小一点，因此将公钥与私钥进行交换，即公钥使用(143, 103)，而私钥使用(143, 7)，设明文为2，则加密过程如下：

3. 用私钥解密

      从以上生成密钥、加密、解密的过程可以看出，虽然我们这里只使用了两个小的素数11和13，但计算量却很大，特别是在加密和解密过程中，需要进行幂运算，得到的结果将是一个非常大的整数。在实际应用中，P、Q要取很大值的素数，则得到的N、D、E值也将很大，所以在加密、解密过程中的幂运算结果将更大，通过C语言(或其他程序设计语言)提供的基本数据类型已经没办法保存这么大的数了。

      因此，RSA算法中，虽然过程很简单，但需要编写程序处理大整数，包括大整数的加、减、乘、除、幂运算等。