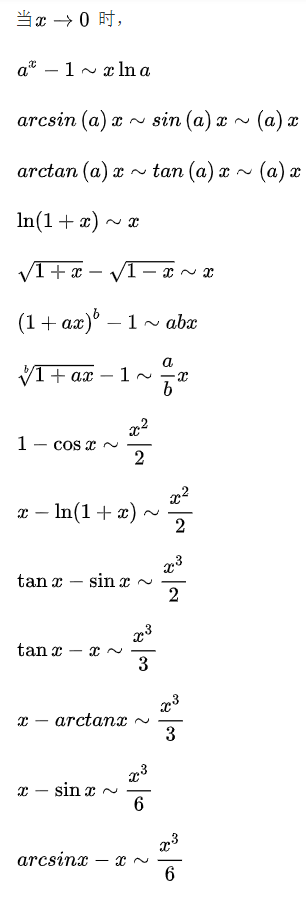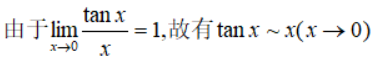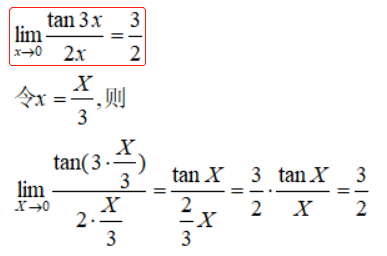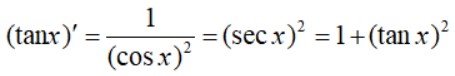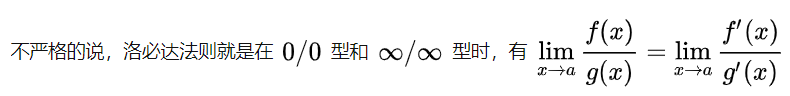1、等价无穷小量代换公式
当无法直接求出极限时,可采用等价无穷小量代换。
等价无穷小代换条件:
(1)被代换的量,在取极限的时候极限值为0。
(2)被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
参见: 百度百科
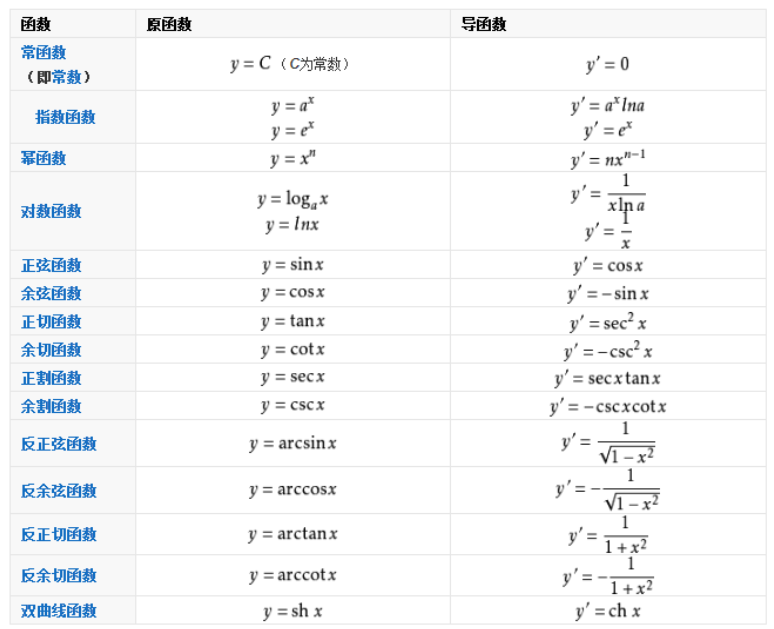
2、三角函数求导公式
如果对分子分母求导后还是0/0型或∞/∞型,可以继续对分子分母求导。
3、导数的四则运算法则
4、判断函数凹凸性
函数的二阶导数大于0,开口向上,函数为凹函数。
函数的二阶导数小于0,开口向下,函数为凸函数。
函数的二阶导数等于0,函数不凹不凸。
5、求函数拐点
步骤:
(1) 求出二阶导数等于0的点。
(2) 求出二阶导数不存在的点。
(3) 从(1)和(2)的结果集中找出左右极限符号相反的点。
5、夹逼定理

当无法直接求极限时,可考虑从两端逼近。
(1)、找出F(x)和G(x),且满足F(x)<=f(x)<=G(x)
(2)、求出x->x0时,F(x)和G(x)的极限值A
(3)、根据(1)和(2)可知,当x->x0时,f(x)的极限值为A
复合函数
已知函数 y=f(u),当u表示为 u=g(x) 时,y作为x的函数可以表示为形如 y=f(g(x)) 的嵌套结构(u和x表示多变量)。这时,嵌套结构的函数 f(g(x)) 称为 f(u) 和 g(x) 的复合函数。
单变量函数的链式法则
已知单变量函数 y=f(u),当u表示为单变量函数 u=g(x) 时,复合函数 f(g(x)) 的导函数可以如下简单地求出来。 $$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$ 这个公式称为单变量函数的复合函数求导公式,也称为链式法则。
多变量函数的链式法则
在多变量函数的情况下,链式法则的思想也同样适用。只要像处理分数一样对导数的式子进行变形即可。然而事情并没有这么简单,因为必须对相关的全部变量应用链式法则。
我们来考察两个变量的情形。
变量z为u、v的函数,如果u、v分别为x、y的函数( 即 u=f1(x,y),v=f2(x,y) ),则z为x、y的函数,此时下式(多变量函数的链式法则)成立。 $$\frac{δz}{δx}=\frac{δz}{δu}\frac{δu}{δx}+\frac{δz}{δv}\frac{δv}{δx}$$ $$\frac{δz}{δy}=\frac{δz}{δu}\frac{δu}{δy}+\frac{δz}{δv}\frac{δv}{δy}$$ 上式在三个以上的变量的情况下也同样成立。
单变量函数的近似公式
$$f'(x)=\lim\limits_{\Delta{x}\to{0}}\frac{f(x+\Delta{x})-f(x)}{\Delta{x}}\tag{导数的定义}$$ 在这个定义式中,$\Delta{x}$为“无限小的值”,不过若将它替换为“微小的值”,也不会造成很大的误差。因而,下式近似成立。 $$f'(x)\fallingdotseq\frac{f(x+\Delta{x})-f(x)}{\Delta{x}}$$ 将上式变形,可以得到以下单变量函数的近似公式。 $$f(x+\Delta{x})\fallingdotseq{f(x)+f'(x)\Delta{x}}\quad(\Delta{x}为微小的数)$$
多变量函数的近似公式
$$f(x+\Delta{x}, y+\Delta{y})\fallingdotseq{f(x,y)+\frac{\partial{f(x,y)}}{\partial{x}}\Delta{x}+\frac{\partial{f(x,y)}}{\partial{y}}}\Delta{y}$$ $$\Delta{z}=f(x+\Delta{x},y+\Delta{y})-f(x,y)$$ $$\Delta{z}\fallingdotseq{\frac{\partial{z}}{\partial{x}}\Delta{x}+\frac{\partial{z}}{\partial{y}}\Delta{y}}$$ 上式对于两个以上变量依然成立。
近似公式的向量表示
多个变量的函数的近似公式,可以表示为两个向量的内积,例如: $$\nabla{z}=\left(\frac{\partial{z}}{\partial{w}},\frac{\partial{z}}{\partial{x}},\frac{\partial{z}}{\partial{y}}\right),\quad\Delta{x}=(\Delta{w},\Delta{x},\Delta{y})$$ 注:$\nabla$通常读作nabla
其它资料