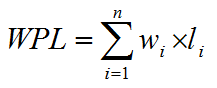哈夫曼树（Huffman Tree）也是一种特殊的二叉树，这种树的所有叶子结点都带有权值，从中构造出带权路径长度最短的二叉树，即哈夫曼树。

设二叉树具有n个带权值的叶子结点，那么从根结点到各个叶子结点的路径长度与相应结点权值的乘积的和，称为二叉树的带权路径长度，记作：

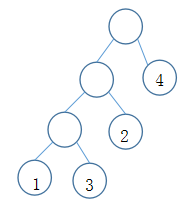
其中，wi为第i个叶子结点的权值；li为第i个叶子结点的路径长度。如图所示的二叉树，它的带权路径长度值WPL=1x3+3x3+2x2+4x1=20。

如果给定一组具有确定权值的叶子结点，可以构造出不同的带权二叉树，它们的带权路径长度并不相同，其中具有最小带权路径长度的二叉树称为哈夫曼树。

哈夫曼树的构造

根据哈夫曼树的定义，一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。那么如何构造一棵哈夫曼树呢？其方法如下。

(1) 由给定的n个权值{W1,W2,...Wn}构造n棵只有一个叶子结点的二叉树，从而得到一个二叉树的集合F={T1,T2,...Tn}。

(2) 在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树，这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。

(3) 在集合F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到集合F中。

(4) 重复 (2)、(3) 两步，当F中只剩下一棵二叉树时，这棵二叉树便是所要建立的哈夫曼树。

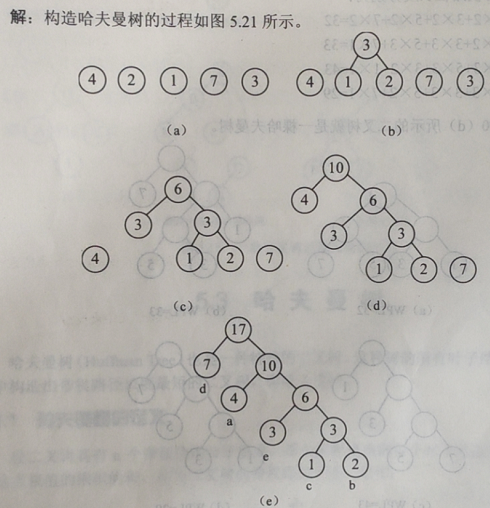
例：对于一组给定的叶子结点{a,b,c,d,e}，它们的权值集合为W={4,2,1,7,3}，给出由此集合构造哈夫曼树的过程。

构造哈夫曼树算法（C语言实现）

typedef struct
{
	char data;   /*结点值*/
	float weight;/*权重*/
	int parent;  /*双亲结点*/
	int lchild;  /*左孩子结点*/
	int rchild;  /*右孩子结点*/
} HTNode;

/*
* 用ht[]数组存放哈夫曼树，对于具有n个叶子结点的哈夫曼树,
* 总共有2n-1个结点。
*/
void CreateHT(HTNode ht[], int n)
{
	int i, j, k, lnode, rnode;
	float min1, min2;
	//所有结点的相关域置初值-1
	//[0,n-1] 存放叶子结点
	//[n, 2n-2] 存放双亲结点(即，非叶子结点)
	for (i = 0;i < 2 * n - 1;i++)
		ht[i].parent = ht[i].lchild = ht[i].rchild = -1;
	//构造哈夫曼树
	for (i = n;i < 2 * n - 1;i++)
	{
		min1 = min2 = 32767;
		//最小权重的两个结点的位置
		lnode = rnode = -1;
		for (k = 0;k <= i - 1;k++)
		{
			//只在尚未构造二叉树的结点中查找
			if (ht[k].parent == -1)
			{
				//找出权重最小的结点
				if (ht[k].weight < min1)
				{
					min2 = min1;
					min1 = ht[k].weight;
					rnode = lnode;
					lnode = k;
				}
				//找出权重次小的结点
				else if (ht[k].weight < min2)
				{
					min2 = ht[k].weight;
					rnode = k;
				}
			}
		}
		ht[lnode].parent = i;
		ht[rnode].parent = i;
		ht[i].weight = ht[lnode].weight + ht[rnode].weight;
		ht[i].lchild = lnode;
		ht[i].rchild = rnode;
	}
	//ht[2n-2]即为哈夫曼树的根结点,也是权重最大的结点。
}