开发工具 Visual Studio2010

Graph.h文件

#define MAXVEX 5	//图中最大顶点数

/////////////////////////////////////////////////////////////////////
//
// 定义邻接表数据结构
//
/////////////////////////////////////////////////////////////////////
 
//定义顶点类型为10个字符的字符数组
typedef char VertexType[10];
 
typedef struct edgenode
{
	int adjvex; //邻接点序号
	int value;  //边的权值
	struct edgenode *next; //下一条边的顶点
} ArcNode; //每个顶点建立的单链表中结点的类型
 
typedef struct vexnode
{
	VertexType data; //顶点信息
	ArcNode *firstarc; //指向第一条边结点
} VHeadNode; //单链表的头结点类型
 
typedef struct
{
	int n,e; //n为实际顶点数，e为实际边数
	VHeadNode adjlist[MAXVEX]; //单链表头结点数组
} AdjList; //图的邻接表类型

/////////////////////////////////////////////////////////////////////
//
// 定义邻接矩阵数据结构
//
/////////////////////////////////////////////////////////////////////

typedef struct vertex
{
	int adjvex;		/*顶点编号*/
	VertexType data;/*顶点信息*/
} VType; /*顶点类型*/
 
typedef struct graph
{
	int n,e; /*n为实际顶点数，e为实际边数*/
	VType vexs[MAXVEX]; /*顶点集合*/
	int edges[MAXVEX][MAXVEX]; /*边的集合*/
} AdjMatix; /*图的邻接矩阵类型*/

GSearch.cpp文件

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include "Graph.h"

//将邻接矩阵g转换成邻接表G*
void MatToList(AdjMatix g, AdjList *&G)
{
	int i,j;
	ArcNode *p;
	G = (AdjList *)malloc(sizeof(AdjList));
	for(i=0; i<g.n; i++) //给邻接表中所有头结点的指针域置初值
	{
		G->adjlist[i].firstarc = NULL;
		strcpy(G->adjlist[i].data, g.vexs[i].data);
	}
	//检查邻接矩阵中每个元素
	for(i=0; i<g.n; i++)
	{
		for(j=g.n - 1; j>=0; j--)
		{
			if(g.edges[i][j] != 0){
				//创建一个结点p
				p = (ArcNode *)malloc(sizeof(ArcNode));
				p->value = g.edges[i][j];
				p->adjvex = j;
				//将p插入到链表之首
				p->next = G->adjlist[i].firstarc;
				G->adjlist[i].firstarc = p;
			}
		}
	}
	G->n = g.n;
	G->e = g.e;
}

void DispAdjList(AdjList *G)
{
	int i;
	ArcNode *p;
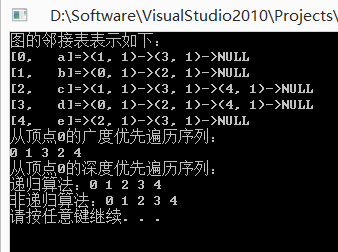
	printf("图的邻接表表示如下：\n");
	for(i=0; i<G->n; i++)
	{
		printf("[%d, %3s]=>", i, G->adjlist[i].data);
		p = G->adjlist[i].firstarc;
		while(p != NULL)
		{
			printf("(%d, %d)->", p->adjvex, p->value);
			p = p->next;
		}
		printf("NULL\n");
	}
}

//对邻接表G从顶点vi开始进行广度优先遍历
void BFS(AdjList *G, int vi)
{
	int i,v,visited[MAXVEX];
	int Qu[MAXVEX], front=0, rear=0; //循环队列
	ArcNode *p;
	for (i=0; i<G->n; i++) //给visited数组置初值0
		visited[i] = 0;
	printf("%d ", vi); //访问初始顶点
	visited[vi] = 1; //置已访问标识
	rear = (rear=1) % MAXVEX; //循环移动队尾指针
	Qu[rear] = vi; //初始顶点进队列
	while (front != rear) //队列不为空时循环
	{
		front = (front + 1) % MAXVEX;
		v = Qu[front]; //顶点v出队
		p = G->adjlist[v].firstarc;//找v的第一个邻接点
		while (p != NULL) //找v的所有邻接点
		{
			if (visited[p->adjvex] == 0) //未访问过则访问它
			{
				visited[p->adjvex] = 1; //置已访问标识
				printf("%d ", p->adjvex);//访问该点并使其入队列
				rear = (rear + 1) % MAXVEX; //循环移动队尾指针
				Qu[rear] = p->adjvex;//顶点p->adjvex进队
			}
			p = p->next; //找v的下一个邻接点
		}
	}
}

//深度优先搜索递归算法
int visited[MAXVEX];
void DFS(AdjList *g, int vi)//对邻接表G从顶点vi开始进行深度优先遍历
{
	ArcNode *p;
	printf("%d ", vi);//访问vi
	visited[vi] = 1; //置已访问标识
	p = g->adjlist[vi].firstarc;//找vi的第一个邻接点
	while (p!=NULL) //找vi的所有邻接点
	{
		if(visited[p->adjvex] == 0){
			DFS(g, p->adjvex); //从vi未访问过的邻接点出发深度优先搜索
		}
		p = p->next;
	}
}
//深度优先搜索非递归算法
void DFS1(AdjList *G, int vi)
{
	ArcNode *p;
	ArcNode *St[MAXVEX];
	int top=-1, v;
	printf("%d ", vi); //访问vi顶点
	visited[vi] = 1; //置已访问标识
	top++; //将初始顶点vi的firstarc指针进栈
	St[top] = G->adjlist[vi].firstarc;
	while (top > -1) //栈不空循环
	{
		p = St[top]; top--;//出栈一个顶点为当前顶点
		while (p!=NULL) //循环搜索其相邻顶点
		{
			v = p->adjvex;//取相邻顶点的编号
			if (visited[v] == 0)//若该顶点未访问过
			{
				printf("%d ", v);//访问v顶点
				visited[v] = 1;//置访问标识
				top++;//将该顶点的第1个相邻顶点进栈
				St[top] = G->adjlist[v].firstarc;
				break; //退出当前顶点的搜索
			}
			p = p->next;//找下一个相邻顶点
		}
	}
}

void main()
{
	int i,j;
	AdjMatix g;
	AdjList *G;
	int a[5][5] = {{0,1,0,1,0},{1,0,1,0,0},{0,1,0,1,1},
					{1,0,1,0,1},{0,0,1,1,0}};
	char *vname[MAXVEX] = {"a", "b", "c", "d", "e"};
	g.n = 5;
	g.e = 12;//建立无向图，每1条无向边算2条有向边
	for(i=0; i<g.n; i++)
		strcpy(g.vexs[i].data, vname[i]);
	for(i=0; i<g.n; i++)
		for(j=0; j<g.n; j++)
			g.edges[i][j] = a[i][j];

	MatToList(g, G);
	DispAdjList(G);

	printf("从顶点0的广度优先遍历序列：\n");
	BFS(G, 0);
	printf("\n");

	for (i=0; i<g.n; i++)
		visited[i] = 0;//顶点标识置初值
	printf("从顶点0的深度优先遍历序列：\n");
	printf("递归算法：");
	DFS(G, 0);
	printf("\n");

	for (i=0; i<g.n; i++)
		visited[i] = 0;//顶点标识置初值
	printf("非递归算法：");
	DFS1(G, 0);
	printf("\n");

	system("pause");
}

工程结构

运行结果