最优化问题和回归分析

作者：追风剑情发布于：2022-6-8 16:44 分类：Algorithms

在为了分析数据而建立数学模型时，通常模型是由参数确定的。在数学世界中，最优化问题就是如何确定这些参数。

从数学上来说，确定神经网络的参数是一个最优化问题，具体就是对神经网络的参数（即权重和偏置）进行拟合，使得神经网络的输出与实际数据相吻合。

为了理解最优化问题，最浅显的例子就是回归分析。下面我们就利用简单的回归分析问题来考察最优化问题的结构。

什么是回归分析

由多个变量组成的数据中，着眼于其中一个特定的变量，用其余的变量来解释这个特定的变量，这样的方法称为回归分析。回归分析的种类有很多，为了理解它的思想，我们来考察一下最简单的一元线性回归分析。

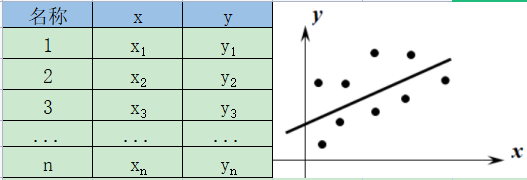
一元线性回归分析是以两个变量组成的数据为考察对象的。下图给出了两个变量x、y的数据以及它们的散点图。

一元线性回归分析是用一条直线近似地表示右图所示的散点图上的点列，通过该直线的方程来考察两个变量之间的关系。

这条近似地表示点列的直线称为回归直线。

这条回归直线用一次关系式表示如下: $$y=px+q \quad (p、q为常数)\tag{1}$$ 这个式子称为回归方程。

x、y是为了将构成数据的各个值代入而设定的变量，右边的x称为自变量，左边的y称为因变量。常数p、q是这个回归分析模型的参数，由给出的数据来决定。

注：p称为回归系数，q称为截矩。

通过具体例子来理解回归分析的逻辑

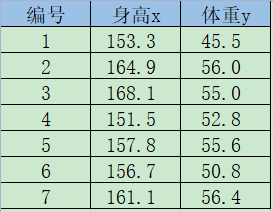
例下图是7个学生的身高与体重数据，求回归方程y=px+q (p、q为常数)

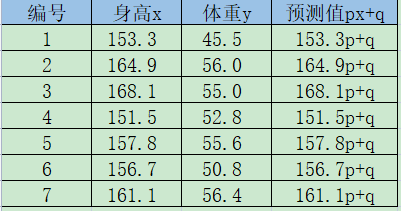
解设所求的回归方程如下所示。 $$y=px+q \quad (p、q为常数)\tag{2}$$ 将第k个学生的身高记为x_k，体重记为y_k，可以求得第k个学生的回归分析预测的值(称为预测值)，如下所示。 $$px_k+q\tag{3}$$ 我们将这些预测值加以汇总，如下表所示。

如下算出实际的体重y_k与预测值的误差e_k。 $$e_k=y_k-(px_k+q)\tag{4}$$

这些e_k的值既可以为正也可以为负。接下来我们来考虑下面的值C_k，这个值称为平方误差。 $$C_k=\frac{1}{2}(e_k)^2=\frac{1}{2}\{y_k-(px_k+q)\}^2\tag{5}$$

注：系数$\frac{1}{2}$是为了方便进行之后的处理，这个值对结论没有影响。

遍历全体数据，将它们的平方差加起来，假设得到的值为C_T。 $$C_T=C_1+C_2+\cdots+C_7$$ 根据之前的表以及式(5)，用p、q的式子表示误差总和C_T，如下所示。 $$ \begin{aligned} C_T&=\frac{1}{2}\{45.5-(153.3p+q)\}^2 + \frac{1}{2}\{56.0-(164.9p+q)\}^2 \\ &+ \cdots +\frac{1}{2}\{50.8-(156.7p+q)\}^2 + \frac{1}{2}\{56.4-(161.1p+q)\}^2 \end{aligned} \tag{6} $$

我们的目标是确定常数p、q的值。回归分析认为，p、q是使误差总和式(6)最小的解。知道这个解的思路后，后面就简单了。我们利用以下的最小值条件即可。 $$\frac{\partial{C_T}}{\partial{p}}=0, \quad \frac{\partial{C_T}}{\partial{q}}=0 \tag{7}$$ 我们来实际计算一下式(6)。根据偏导数的链式法则，可得 $$ \begin{aligned} \frac{\partial{C_T}}{\partial{p}}&=-153.3\{45.5-(153.3p+q)\} - 164.9\{56.0-(164.9p+q)\}- \\ &\cdots -156.7\{50.8-(156.7p+q)\} - 161.1\{56.4-(161.1p+q)\}=0 \\ \frac{\partial{C_T}}{\partial{q}}&=-\{45.4-(153.3p+q)\} - \{56.0-(164.9p+q)\} - \\ &\cdots -\{50.8-(156.7p+q)\} - \{56.4-(161.1p+q)\}=0 \end{aligned} $$ 整理后得到下式。 $$ 1113.4p+7q=372.1, \quad 177312p+1113.4q=59274 $$ 解这个联立方程，可得 $$p=0.41,\quad q=-12.06$$ 从而求得目标回归方程(2)，如下所示。 $$y=0.41x-12.06$$

注：这是C_T=27.86

以上就是一元线性回归分析中使用的回归直线的确定方法。这里的重点是最优化问题的求解思路。这里所考察的最优化方法在后面的神经网络的计算中也可以直接使用。

注意：要确定模型，就必须准备好规模大于参数个数的数据。