鸟语天空

狄克斯特拉(Dijkstra)算法

作者：追风剑情 发布于：2014-8-2 20:15 分类：Algorithms

Dijkstra是求解某点到其他各点的最短路径算法。

开发工具 Visual Studio2010

#include <stdlib.h>
#include <stdio.h>

const int MAXVEX = 6;//最大顶点数
const int INF = 429496729;//无路径时的权值

/**
 * 狄克斯特拉算法
 * @param cost 图的代价矩阵
 * @param n    图的顶点数
 * @param v    源点(起点)编号
 */
void Dijkstra(int cost[][MAXVEX], int n, int v)
{
	int dist[MAXVEX], path[MAXVEX];
	int s[MAXVEX];
	int mindis, i, j, u, pre;
	for(i=0; i<n; i++)
	{
		dist[i] = cost[v][i]; //初始化距离
		s[i] = 0; //置空s[]

		//初始化路径
		if(cost[v][i] < INF)
			path[i] = v;
		else
			path[i] = -1;
	}

	s[v] = 1; //源点编号v放入s中
	path[v] = 0;
	//循环直到所有顶点的最短路径都求出
	for(i=0; i<n; i++)
	{
		mindis = INF;
		u = -1;
		for(j=0; j<n; j++) //选取不在s中且具有最小距离的顶点u
		{
			if(s[j] == 0 && dist[j] < mindis)
			{
				u = j;
				mindis = dist[j];
			}
		}

		if (u != -1) //找到最小距离的顶点u
		{
			s[u] = 1; //顶点u加入s中
			for (j=0; j<n; j++) //修改不在s中的顶点距离
			{
				if (s[j] == 0)
				{
					if (cost[u][j] < INF && dist[u] + cost[u][j] < dist[j])
					{
						dist[j] = dist[u] + cost[u][j];//修改源点到vj的距离
						path[j] = u;//保存当前最短路径中的前一个顶点编号
					}
				}
			}
		}
	}

	printf("\n Dijkstra算法求解如下：
");
	//输出最短路径长度，路径逆序输出
	for (i=0; i<n; i++)
	{
		printf("%d->%d：", v, i);
		if (i != v)
		{
			if (s[i] == 1)
			{
				printf("路径长度为%2d ", dist[i]);
				pre = i;
				printf("路径逆序为");
				while (pre != v) //直到求解到初始顶点
				{
					printf("%d, ", pre);
					pre = path[pre];
				}
				printf("%d\n", pre);
			}else{
				printf("不存在路径
");
			}
		}else{
			printf("不存在路径
");
		}
	}

	printf("\n");
}

void main()
{
	//定义一个代价矩阵作为测试数据 INF:无路径
	int cost[6][MAXVEX] = {
		{0,   50,  10,  INF, INF, INF},
		{INF, 0,   15,  50,  10,  INF},
		{20,  INF, 0,   15,  INF, INF},
		{INF, 20,  INF, 0,   35,  INF},
		{INF, INF, INF, 30,  0,   INF},
		{INF, INF, INF, 3,   INF, 0  }
	};

	Dijkstra(cost, 6, 1);

	system("pause");
}

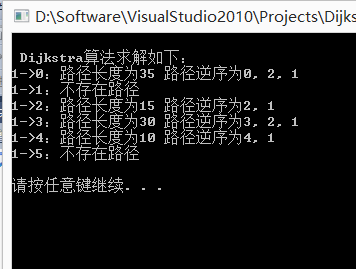
运行效果

标签: Algorithms