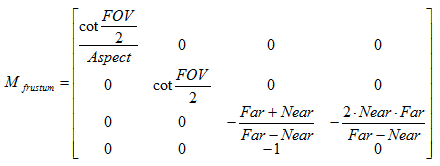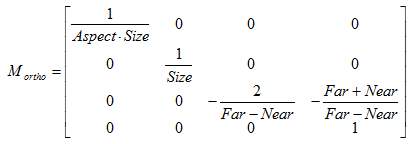裁剪空间

作者：追风剑情发布于：2016-12-26 22:20 分类：Shader

顶点接下来要从观察空间转换到裁剪空间(clip space，也被称为齐次裁剪空间)中，这个用于转换的矩阵叫做裁剪矩阵(clip matrix)，也被称为投影矩阵(projection matrix)。

裁剪空间的目标是能够方便地对渲染图元进行裁剪：完全位于这块空间内部的图元将会被保留，完全位于这块空间外部的图元将会被剔除，而与这块空间边界相交的图元就会被裁剪。那么，这块空间是如何决定的呢？答案是由视锥体(view frustum)来决定。

视锥体指的是空间中的一块区域，这块区域决定了摄像机可以看到的空间。视锥体由六个平面包围而成，这些平面也被称为裁剪平面(clip planes)。视锥体有两种类型，这涉及两种投影类型：一种是正交投影(orthographic projection)，一种是透视投影(perspective projection)。

在视锥体的6块裁剪平面中，有两块裁剪平面比较特殊，它们分别被称为近裁剪平面(near clip plane)和远裁剪平面(far clip plane)。它们决定了摄像机可以看到的深度范围。

透视投影

正交投影

前面讲到，我们希望根据视锥体转成的区域对图元进行裁剪，但是，如果直接使用视锥体定义的空间来进行裁剪，那么不同的视锥体就需要不同的处理过程，而且对于透视投影的视锥体来说，想要判断一个顶点是否处于一个金字塔内部是比较麻烦的。因此，我们想用一种更加通用、方便和整洁的方式来进行裁剪的工作，这种方式就是通过一个投影矩阵把顶点转换到一个裁剪空间中。

投影矩阵有两个目的：

首先是为投影做准备。这是个迷惑点，虽然投影矩阵的名称包含了投影二字，但是它并没有进行真正的投影工作，而是在为投影做准备。真正的投影发生在后面的齐次除法(homogeneous division)过程中。而经过投影矩阵的变换后，顶点的w分量将会具有特殊的意义。
其次是对x、y、z分量行进缩放。我们上面讲过直接使用视锥体的6个裁剪平面来进行裁剪会比较麻烦。而经过投影矩阵的缩放后，我们可以直接使用w分量作为一个范围值，如果x、y、z分量都位于这个范围内，就说明该顶点位于裁剪空间内。

读者：投影到底是什么意思呢？
我们：可以理解成是一个空间的降维，例如从四维空间投影到三维空间中。而投影矩阵实际上并不会真的进行这个步骤，它会为真正的投影做准备工作。真正的投影会在屏幕映射时发生，通过齐次除法来得到二维坐标。

在裁剪空间之前，虽然我们使用了齐次坐标来表示点和矢量，但它们的第四个分量都是固定的：点的w分量是1，方向矢量的w分量是0。经过投影矩阵的变换后，我们就会赋予齐次坐标的第4个坐标更加丰富的含义。下面，我们来看一下两种投影类型使用的投影矩阵具体是什么。

透视投影

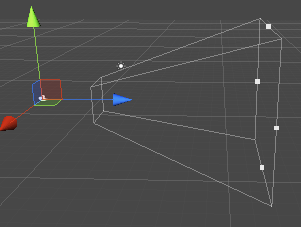
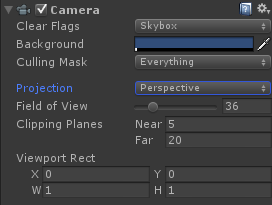
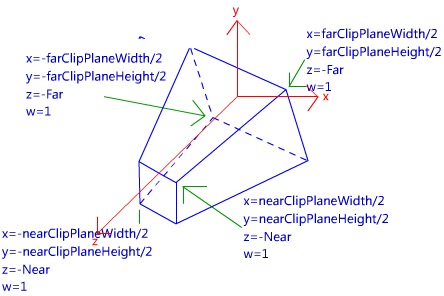
视锥体的意义在于定义了场景中的一块三维空间。所有位于这块空间内的物体将会被渲染，否则就会被剔除或裁剪。我们已经知道，这块区域由6个裁剪平面定义，那么这6个裁剪平面又是怎么决定的呢？在Unity中，它们由Camera组件中的参数和Game视图的横纵比共同决定。

由图可以看出，我们可以通过Camera组件的Field of View(简称FOV)属性来改变视锥体竖直方向的张开角度，而Clipping Planes中的Near和Far参数可以控制视锥体的近裁剪平面和远裁剪平面距离摄像机的远近。这样，我们可以求出视锥体近裁剪平面和远裁剪平面的高度，也就是：

nearClipPaneHeight=2●Near●tan(FOV/2)
farClipPlaneHeight=2●Far●tan(FOV/2)
现在我们还缺乏横向的信息。这可以通过摄像机的横纵比得到。在Unity中，一个摄像机的横纵比由Game视图的横纵比和Viewport Rect中的W和H属性共同决定(实际上，Unity允许我们在脚本里通过Camera.aspect进行更改，但这里不做讨论)。假设，当前摄像机的横纵比为Aspect，我们定义：

Aspect=nearClipPlaneWidth/nearClipPlaneHeight
Aspect=farClipPlaneWidth/farClipPlaneHeight
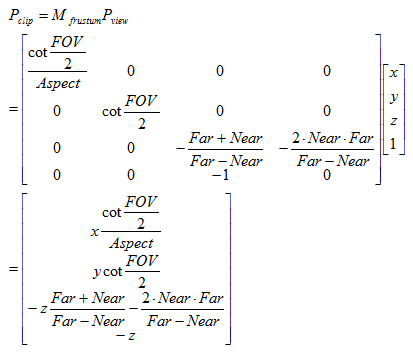
现在，我们可以根据已知的Near、Far、FOV和Aspect的值来确定透视投影的投影矩阵。如下：

需要注意的是，这里的投影矩阵是建立在Unity对坐标系的假定上面的，也就是说，我们针对的是观察空间为右手坐标系，使用列矩阵在矩阵右侧进行相乘，且变换后z分量范围将在[-w, w]之间的情况。而在类似DirectX这样的图形接口中，它们希望变换后z分量范围将在[0, w]之间，因此就需要对上面的透视矩阵进行一些更改。

而一个顶点和上述投影矩阵相乘后，可以由观察空间变换到裁剪空间中，结果如下：

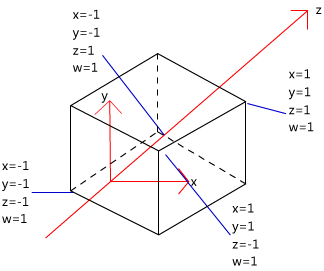
从结果可以看出，这个投影矩阵本质就是对x、y和z分量进行了不同程度的缩放(当然，z分量还做了一个平移)，缩放的目的是为了方便裁剪。我们可以注意到，此时顶点的w分量不再是1，而是原先z分量的取反结果。现在，我们就可以按如下不等式来判断一个变换后的顶点是否位于视锥体内。如果一个顶点在视锥体内，那么它变换后的坐标必须满足：
-w≤x≤w
-w≤y≤w
-w≤z≤w
任何不满足上述条件的图元都需要被剔除或者裁剪。

从上图还可以注意到，裁剪矩阵会改变空间的旋向性：空间从右手坐标系变换到了左手坐标系。这意味着，离摄像机越远，z值将越大。

正交投影

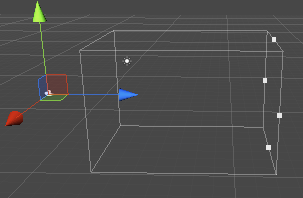
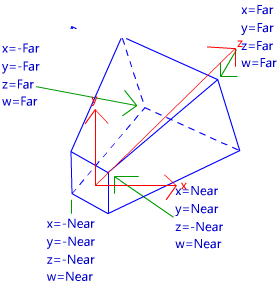
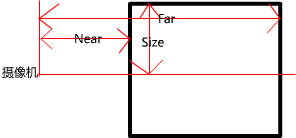
首先，我们还是看一下正交投影中的6个裁剪平面是如何定义的。和透视投影类似，在Unity中，它们也是由Camera组件中的参数和Game视图的横纵比共同决定。

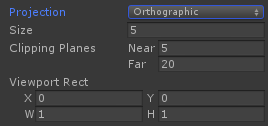
正交投影的视锥体是一个长方体，因此计算上相比透视投影来说更加简单。由图可以看出，我们可以通过Camera组件的Size属性来改变视锥体竖直方向上高度的一半，而Clipping Planes中的Near和Far参数可以控制视锥体的近裁剪平面和远裁剪平面距离摄像机的远近。这样，我们可以求出视锥体近裁剪平面和远裁剪平面的高度，也就是：
nearClipPlaneHeight=2●Size
farClipPlaneHeight=nearClipPlaneHeight
现在我们还缺乏横向的信息。同样，我们可以通过摄像机的横纵比得到。假设，当前摄像机的横纵比为Aspect，那么：
nearClipPlaneWidth=Aspect●nearClipPlaneHeight
farClipPlaneWidth=nearClipPlaneWidth
现在，我们可以根据已知的Near、Far、Size和Aspect的值来确定正交投影的裁剪矩阵。如下: