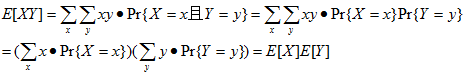随机变量的期望值
作者:追风剑情 发布于:2016-12-15 15:06 分类:Algorithms
期望值一个随机变量的期望值是变量的输出值乘以其机率的总和,换句话说,期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。
当该和是有限的或绝对收敛时,它是有定义的。有时,X的期望可以表示为μx,或者当随机变量在上下文中显然时,可以简写为μ。
考虑扔两枚均匀硬币的游戏。游戏者对于每枚正面朝上的硬币可以赢3美元,对于每枚反面朝上的硬币输掉2美元。表示收入的随机变量X的期望是
E[X]=6●Pr{2H}+1●Pr{1H, 1T}-4●Pr{2T}=6(1/4)+1(1/2)-4(1/4)=1
两个随机变量的和的期望与它们期望之和相等,即
E[X+Y]=E[X]+E[Y]
其中,E[X]与E[Y]需要有定义,我们称这个性质为期望的线性性质,并且即使X与Y不独立,该性质也成立。这一性质可以扩展到有限的以及绝对收敛的期望和上。期望的线性性质是允许我们使用指标随机变量进行概率分析的关键性质。
如果X是随机变量,任何函数g(x)定义一个新的随机变量g(X)。如果g(x)的期望有定义,则
令g(x)=ax,则对于任意常数a,E[aX]=aE[X],所以,期望是线性的:对于任意两个随机变量X和Y以及任意常数a,有E[aX+Y]=aE[X]+E[Y]
当两个随机变量X和Y独立且期望有定义时,
通常,当n个随机变量X1,X2,...,Xn互相独立时,E[X1X2...Xn]=E[X1]E[X2]...E[Xn]
当随机变量X可在自然数集N={0, 1, 2, ...}中取值时,有一个很好的期望计算公式:
因为在公式推导过程中,每一项Pr{X≥i}被加了i次,又被减了i-1次(除了Pr{X≥0},它被加0次,从未被减过。
当我们将一个凸函数f(x)应用到随机变量X上时,假定期望存在且有限,由詹森不等式得E[f(X)]≥f(E[X])
如果对于所有x,y和所有0≤λ≤1,有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y),则函数f(x)是凸函数。
标签: Algorithms
日历
最新文章
随机文章
热门文章
分类
存档
- 2025年3月(4)
- 2025年2月(3)
- 2025年1月(1)
- 2024年12月(5)
- 2024年11月(5)
- 2024年10月(5)
- 2024年9月(3)
- 2024年8月(3)
- 2024年7月(11)
- 2024年6月(3)
- 2024年5月(9)
- 2024年4月(10)
- 2024年3月(11)
- 2024年2月(24)
- 2024年1月(12)
- 2023年12月(3)
- 2023年11月(9)
- 2023年10月(7)
- 2023年9月(2)
- 2023年8月(7)
- 2023年7月(9)
- 2023年6月(6)
- 2023年5月(7)
- 2023年4月(11)
- 2023年3月(6)
- 2023年2月(11)
- 2023年1月(8)
- 2022年12月(2)
- 2022年11月(4)
- 2022年10月(10)
- 2022年9月(2)
- 2022年8月(13)
- 2022年7月(7)
- 2022年6月(11)
- 2022年5月(18)
- 2022年4月(29)
- 2022年3月(5)
- 2022年2月(6)
- 2022年1月(8)
- 2021年12月(5)
- 2021年11月(3)
- 2021年10月(4)
- 2021年9月(9)
- 2021年8月(14)
- 2021年7月(8)
- 2021年6月(5)
- 2021年5月(2)
- 2021年4月(3)
- 2021年3月(7)
- 2021年2月(2)
- 2021年1月(8)
- 2020年12月(7)
- 2020年11月(2)
- 2020年10月(6)
- 2020年9月(9)
- 2020年8月(10)
- 2020年7月(9)
- 2020年6月(18)
- 2020年5月(4)
- 2020年4月(25)
- 2020年3月(38)
- 2020年1月(21)
- 2019年12月(13)
- 2019年11月(29)
- 2019年10月(44)
- 2019年9月(17)
- 2019年8月(18)
- 2019年7月(25)
- 2019年6月(25)
- 2019年5月(17)
- 2019年4月(10)
- 2019年3月(36)
- 2019年2月(35)
- 2019年1月(28)
- 2018年12月(30)
- 2018年11月(22)
- 2018年10月(4)
- 2018年9月(7)
- 2018年8月(13)
- 2018年7月(13)
- 2018年6月(6)
- 2018年5月(5)
- 2018年4月(13)
- 2018年3月(5)
- 2018年2月(3)
- 2018年1月(8)
- 2017年12月(35)
- 2017年11月(17)
- 2017年10月(16)
- 2017年9月(17)
- 2017年8月(20)
- 2017年7月(34)
- 2017年6月(17)
- 2017年5月(15)
- 2017年4月(32)
- 2017年3月(8)
- 2017年2月(2)
- 2017年1月(5)
- 2016年12月(14)
- 2016年11月(26)
- 2016年10月(12)
- 2016年9月(25)
- 2016年8月(32)
- 2016年7月(14)
- 2016年6月(21)
- 2016年5月(17)
- 2016年4月(13)
- 2016年3月(8)
- 2016年2月(8)
- 2016年1月(18)
- 2015年12月(13)
- 2015年11月(15)
- 2015年10月(12)
- 2015年9月(18)
- 2015年8月(21)
- 2015年7月(35)
- 2015年6月(13)
- 2015年5月(9)
- 2015年4月(4)
- 2015年3月(5)
- 2015年2月(4)
- 2015年1月(13)
- 2014年12月(7)
- 2014年11月(5)
- 2014年10月(4)
- 2014年9月(8)
- 2014年8月(16)
- 2014年7月(26)
- 2014年6月(22)
- 2014年5月(28)
- 2014年4月(15)
友情链接
- Unity官网
- Unity圣典
- Unity在线手册
- Unity中文手册(圣典)
- Unity官方中文论坛
- Unity游戏蛮牛用户文档
- Unity下载存档
- Unity引擎源码下载
- Unity服务
- Unity Ads
- wiki.unity3d
- Visual Studio Code官网
- SenseAR开发文档
- MSDN
- C# 参考
- C# 编程指南
- .NET Framework类库
- .NET 文档
- .NET 开发
- WPF官方文档
- uLua
- xLua
- SharpZipLib
- Protobuf-net
- Protobuf.js
- OpenSSL
- OPEN CASCADE
- JSON
- MessagePack
- C在线工具
- 游戏蛮牛
- GreenVPN
- 聚合数据
- 热云
- 融云
- 腾讯云
- 腾讯开放平台
- 腾讯游戏服务
- 腾讯游戏开发者平台
- 腾讯课堂
- 微信开放平台
- 腾讯实时音视频
- 腾讯即时通信IM
- 微信公众平台技术文档
- 白鹭引擎官网
- 白鹭引擎开放平台
- 白鹭引擎开发文档
- FairyGUI编辑器
- PureMVC-TypeScript
- 讯飞开放平台
- 亲加通讯云
- Cygwin
- Mono开发者联盟
- Scut游戏服务器引擎
- KBEngine游戏服务器引擎
- Photon游戏服务器引擎
- 码云
- SharpSvn
- 腾讯bugly
- 4399原创平台
- 开源中国
- Firebase
- Firebase-Admob-Unity
- google-services-unity
- Firebase SDK for Unity
- Google-Firebase-SDK
- AppsFlyer SDK
- android-repository
- CQASO
- Facebook开发者平台
- gradle下载
- GradleBuildTool下载
- Android Developers
- Google中国开发者
- AndroidDevTools
- Android社区
- Android开发工具
- Google Play Games Services
- Google商店
- Google APIs for Android
- 金钱豹VPN
- TouchSense SDK
- MakeHuman
- Online RSA Key Converter
- Windows UWP应用
- Visual Studio For Unity
- Open CASCADE Technology
- 慕课网
- 阿里云服务器ECS
- 在线免费文字转语音系统
- AI Studio
- 网云穿
- 百度网盘开放平台
- 迅捷画图
- 菜鸟工具
- [CSDN] 程序员研修院
- 华为人脸识别
- 百度AR导航导览SDK
- 海康威视官网
- 海康开放平台
- 海康SDK下载
- git download
- Open CASCADE
- CascadeStudio
交流QQ群
-
Flash游戏设计: 86184192
Unity游戏设计: 171855449
游戏设计订阅号